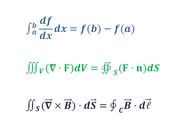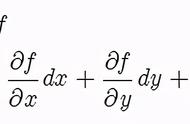粘度为μ,密度为ρ的不可压缩牛顿流体,受静水压力p和加速度g的作用,其运动可以描述为满足纳维尔(叶)-斯托克斯(Navier-Stokes)方程的速度矢量场V:

- 我们用复数形式来表示这一个方程,因为它以向量的形式表示了三个方程
这些方程式是以克劳德-路易·纳维尔和乔治·斯托克斯爵士的名字命名的。
纳维尔-斯托克斯方程方程是一个微分方程,它对空间中每一点的无限小流体的速度V施加规则。结果可以解释为浸没在流体中的测试粒子的运动或流体本身的运动。
假设V的x,y,z分量分别为u,v,w。单位向量在x,y和z方向将被写成x,y和z。
如果你上过一些基础的物理或微积分课程,你可能会认识∇算子,并理解标量函数的拉普拉斯函数∇²f和向量函数的散度∇⋅F 。在纳维尔-斯托克斯方程中有两个向量微分算子,你们可能不熟悉。第一个是矢量拉普拉斯运算符∇²V,第二个是运算符 (V⋅∇)V。幸运的是,我们很容易理解这些运算符的含义。拉普拉斯向量对向量函数的每个标量分量应用拉普拉斯算子:

变形是使一个物质体的所有组成粒子发生位移的过程。这里,我们感兴趣的是连续变形。在这种变形中,物质体不会被分离成不相交的部分。在这种变形之前,粒子之间的距离是无穷小的,在变形之后,粒子之间的距离仍然是无穷小的。
物体的变形是由表面的应力引起的,表面应力有两种类型。正应力的方向垂直于表面,剪应力的方向平行于表面。应力等于力除以面积。
流体被定义为不能抵抗剪应力的物质体。只要对某一流体体施加剪应力,该流体就会不断地变形。这就引出了流体的流行定义,即流体总是以其容器的形状存在。牛顿体是一种变形的变化率与应力成线性关系的流体。