在中我们介绍了均值不等式的一些基本知识,这篇文章继续介绍不等式的另一个重要知识点—柯西不等式。
一、柯西不等式的形式及记忆技巧- 代数形式
(1)二维:设,当且仅当时取等号。
(2)多维:,当且仅当时取等号。
(3)记忆技巧:平方项比交叉项要大一些,不等式两边的总幂次一致。
- 向量形式
设向量,则,当且仅当两个向量共线时取等号。
记忆技巧:根据向量点积和模长计算方法即可自然得到。
- 三角形式
设则,即,当且仅当P1、P2、O三点共线且P1、P2在O点两侧时取等号。
记忆技巧:三角形两边之和大于第三边。
- 柯西不等式的证明
关于柯西不等式的证明有很多精妙的方法,向量形式和三角形式几乎是不证自明的,本文仅给出多维代数形式的一种证明方法。
证明:构造函数,展开可得
由于,可得
化简可得
取等号的条件是方程有两个相同的解,此时有:
(此时方程的解为0)或
,即
二、常见题型利用柯西不等式的核心有两点:一是注意拼凑,在已知条件和要求的式子之间寻找联系;二是注意不等式两边幂次的变化,这里同样需要注意常数的应用,在不知不觉间完成升幂或者降幂,进而使问题得解或者最起码使问题得以简化。
1.求最大值(定高幂次,求低幂次)
例1:设
解析:直接套用柯西不等式
当且仅当时取等号。
例2:已知正数
解析:要求的式子与已知条件并不是直接的平方关系,不能直接套用例1 的方法。考虑柯西不等式的向量形式,设,则
又
则有
∴,而
思考:(1)均值不等式也具有幂次变化的功能,用均值不等式证明该题是否可行?
(2)已知条件改为,结论是否仍然成立?
在处理给定高幂次的题型时,要注意发掘隐含的高幂次等式。
例3:求函数的最大值
解析:辅助角公式可以直接求解,这里我们采用柯西不等式
当且仅当时取等号。
例4:求函数
解析:显然,易求最大值为.
2.求最小值(定低幂次,求高幂次)
例5:实数
解析:,当且仅当时取等号。
∴。
例6:已知
解析:,当且仅当时取等号
∴.
例7:已知
解析:由于系数的关系,此题比前两个例题稍显复杂,但本质是一样的
,当且仅当时取等号
∴
3.分式型
如果分母的和为定值,则乘以该定值可以对分式进行有效简化,该方法类似于中提到的妙用常数法。
例8:已知正实数
解析:利用均值不等式中的妙用常数法可以解决这类问题,此处介绍柯西不等式的方法。
,当且仅当时取等号。
因此所求最小值为25/8.
例9:已知正数,求证
解析:分母之和为定值3,给分式乘以分母之和,有
,即可得证。
此题采用均值不等式也可以做,但是当项数较多时,直接采用柯西不等式更加简单明了。
上述例题属于基本题型,分母之和为定值,掌握柯西不等式的基本形式一般都能轻松应对。有时候题目的条件与所求结果之间可能需要一定的处理才能达到应用柯西不等式的条件。
✳例10:已知正常数
解析:此题三角函数在分母上,不能直接套用柯西不等式。分析可知,我们需要给y乘以一个关于正弦和余弦函数的线性组合,即可初步得到最小值,即
,
当且仅当时取等号.进一步根据三角恒等式,化为给定高幂次的情形,即
,当且仅当时取等号
两个取等条件同时成立,可得,不妨令
解:
∵
当且仅当时取等号
,当且仅当时取等号
∴,即
,当且仅当时取等号
所以y的最小值为
4.分离参数法(多参数)
求某参数的取值范围,一般需要将该参数分离出来,进而利用柯西不等式。
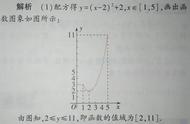
例11:已知,求y的取值范围。
解析:分离参数y至等式的一边,可得
解得
5.待定系数法
这类方法常用于含有根式与一次项的和式,
例12:已知
解析:若能得到的形式,则可得到的形式,为所求函数运用柯西不等式创造条件。
取参数,则
∴,即
(1)
∴ (2)
联立式(1)、(2)的取等条件
解得
此时y取得最小值4.
例13:已知正实数的最小值。
解析:为了向已知条件靠拢,最终应凑成的形式。因此,应用柯西不等式对所求函数进行变形处理。引入参数
,取等条件 (1)
,取等条件 (2)
∴
为了应用已知条件,令
(3)
联立(1)、(2)、(3)及已知条件,解得
所以
6.取等条件在方程组中的应用
有时候题目给定的未知数数量多于方程数量时应有所警觉,注意取等条件,这里需要有一定的数学直觉。
例14:解实数方程组
解析:3个未知数两个方程,常规方法无法求解方程组,但是根据柯西不等式可知
而,即上式取到等号
∴
易求出
例15:实数,则
解析:未知数数量多于方程数量,考虑不等式取等号的条件
∵
而题中已知
∴
解得
三、小结柯西不等式可以在不同幂次的代数式之间构建桥梁,解题时应注意通过一定的变形在已知条件和要求的问题之间建立联系,有时候可能需要不止一次的应用不等式(注意不等式的方向和取等条件),应时刻关注取等条件,尤其在未知数数量多余方程数量的条件下,取等条件可能就是破题的关键。