首先解读一下规则,除了字面上看到的意思,还隐藏了哪些意思呢?
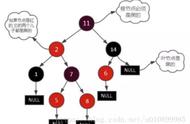
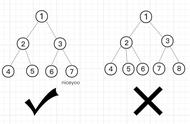
①从根节点到叶子节点的最长路径不大于最短路径的 2 倍
怎么样的路径算最短路径?从规则 5 中,我们知道从根节点到每个叶子节点的黑色节点数量是一样的,那么纯由黑色节点组成的路径就是最短路径。
什么样的路径算是最长路径?根据规则 4 和规则 3,若有红色节点,则必然有一个连接的黑色节点,当红色节点和黑色节点数量相同时,就是最长路径,也就是黑色节点(或红色节点)*2。
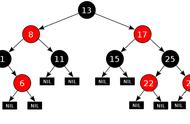
②为什么说新加入到红黑树中的节点为红色节点
从规则 4 中知道,当前红黑树中从根节点到每个叶子节点的黑色节点数量是一样的,此时假如新的是黑色节点的话,必然破坏规则。
但加入红色节点却不一定,除非其父节点就是红色节点,因此加入红色节点,破坏规则的可能性小一些,下面我们也会举例来说明。
什么情况下,红黑树的结构会被破坏呢?破坏后又怎么维持平衡,维持平衡主要通过两种方式【变色】和【旋转】,【旋转】又分【左旋】和【右旋】,两种方式可相互结合。
下面我们从插入和删除两种场景来举例说明。
红黑树节点插入
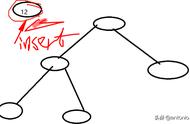
当我们插入值为 66 的节点时,红黑树变成了这样:

很明显,这个时候结构依然遵循着上述 6 大规则,无需启动自动平衡机制调整节点平衡状态。
如果再向里面插入值为 51 的节点,这个时候红黑树变成了这样:

很明显现在的结构不遵循规则 4 了,这个时候就需要启动自动平衡机制调整节点平衡状态。
变色
我们可以通过变色的方式,使结构满足红黑树的规则:
- 首先解决结构不遵循规则 4 这一点(红色节点相连,节点 49-51),需将节点 49 改为黑色。
- 此时我们发现又违反了规则 5(56-49-51-XX 路径中黑色节点超过了其他路径),那么我们将节点 45 改为红色节点。
- 哈哈,妹的,又违反了规则 4(红色节点相连,节点 56-45-43),那么我们将节点 56 和节点 43 改为黑色节点。
- 但是我们发现此时又违反了规则 5(60-56-XX 路径的黑色节点比 60-68-XX 的黑色节点多),因此我们需要调整节点 68 为黑色。
- 完成!

最终调整完成后的树为: