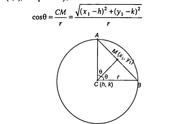
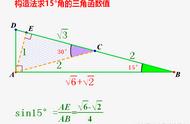
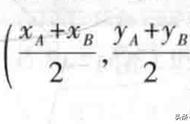新知应用答案
在几何中,平行四边形对角线互相平分,常常利用这一条原理来应用这个公式。
换句话说,只要出现中点,都可以利用这个公式来解题。
像三角形的中线、直角三角形的斜边中线、垂直平分线、圆的直径求圆心等,只要出现中点,都应想到是否能用这个公式来解题?
拓展应用拓展,其在二次函数中抛物线变换中的应用。

拓展
提示:旋转180°,中心对称,应想到两点之间中点坐标公式。
解答如下图:

拓展解答1
前两问,解题关键在于读懂什么叫关联二次函数,旋转180°,说明两个顶点成中心对称,可先求出C1的顶点(1,-2),又因为关于(t,-1)中心对称,所以C2的顶点坐标为(2t-1,0),再把C2代入C1解析式,求解,即可。
计算技巧:知道中点,中点2倍减已知就可以了。
例此题,x=2t-1,y=-1×2-(-2)=0.
第(3)、(4)问答案如下图:

拓展解答2
解题关键还是中点坐标公式的应用。
牛刀小试试一试,方法如故。
第一题:公式巩固,如下图: