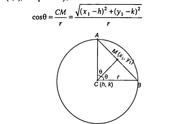
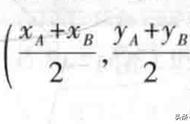在初中阶段,经常涉及到 30°,45°,60°等特殊角的三角函数值的运算,实际上15°角也算是一个常用的特殊角,其三角函数值比较复杂,在初中阶段,常常采用构造法来推导。下面提供四种构造方法(推荐用方法二),有繁有简,都涉及到二次根式的化简以及双重根号的化简,因此,在中考考纲中是不作要求的,但其中的构造法还是值得学习的。欢迎提供更好的构造方法。
方法一:30°=2×15°,构造30°角来求 (稍繁琐)描述:取BD中点C,根据直角三角形斜边的中线等于斜边的一半,可以知道AC=CB,那么∠CAB=∠B=15°,再根据三角形外角定理:三角形的外角等于与它不相邻的两个内角的和,可以知道∠ACE=30°,再经过A点作AE⊥BD于E,则成功构造出了一个含有30°角的直角三角形ACE 。为了计算的方便,不妨令 AE=1,则AC=2 (根据:在直角三角形中,30°角所对的直角边等于斜边的一半) ,从而BC=2,CE=√3,再根据勾股定理求出AB=√6 √2 ,在直角三角形ABE中,三边的长度都知道了,可以根据锐角三角函数的定义,求出15°角的三个函数值。