初中几何经常会遇到题目中给出角平分线的问题,解题目标往往是边长之间关系。其实这类问题的解题方向非常明确,角平分线与边长相关的性质比较常用的只有三个,其中角平分长公式可以不掌握,也就是把角平分线的两个性质用活就行。这里按重要性程度的顺序总结一下。
定理1:角平分线上的点到这个角两边的距离相等。
定理1的逆定理:在角的内部到一个角的两边距离相等的点在这个角的角平分线上。
这个证明是非常简单直观的。

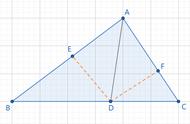
在△ABC中,AD是∠BAC的角平分线。那么过D做AB和AB的垂线,垂足分别为E和F。
因为∠BAD=∠CAD(角平分线),∠AED=∠AFD=90°,AD=AD
那么△AED与△AFD全等,于是有DE=DF。证毕。
同理,也通过证明三角形全等证明其逆定理。
定理2:在△ABC中,AD是∠BAC的平分线,则AB/BD=AC/CD
(也可表示为AB/AC =BD/CD)。
定理2的逆定理: 在△ABC中,若 AB/BD=AC/CD,则AD是∠BAC的平分线。

这个定理的描述非常简单优美,证明需要一点小技巧。
证明:
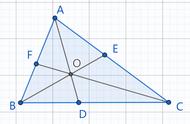
在△ABC中,AD是∠BAC的平分线
过点D作DE⊥AB,DF⊥AC

∵AD是∠BAC的平分线,DE⊥AB,DF⊥AC
∴DE=DF
∵2S△ABD=AB×DE且2S△ACD=AC×DF
∴S△ABD:S△ACD=AB:AC
又∵S△ABD:S△ACD=BD:CD(同高,面积比例为底边比例)
∴S△ABD:S△ACD=AB:AC=BD:CD
∴AB:AC=BD:CD
定理3:在△ABC中,AD是∠BAC的平分线,则AD²=AB×AC-BD×CD(角平分线长公式)

这个定理的证明方法超出中学阶段教材的内容范畴,有兴趣的可以去研究一下几何中著名的斯特瓦尔特定理,根据斯特瓦尔特定理和角平分线的性质可以证明。
,