本文解一道网红小学几何题,适合初中学历读者。
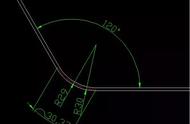
问题如图,正方形 ABCD 的边长为 10,正方形内部有一个内切圆,分别以 A、C 为圆心,正方形边长为半径画弧,求两条弧与圆所夹的阴影部分面积。

方法一:几何方法
如图,由于整个图形关于直线 AD 对称,故阴影部分面积可以看成左上、右下两个完全一样的阴影部分面积组成,这里我们只求左上阴影部分面积。正方形 ABCD 的中心为 O,这也是内切圆的圆心,弧 BD 交内切圆于 E、F 两点,连接 OE、OF、OC、CE、CF。

注意到的三条边都是已知的,其中
故我们解可得:
根据二倍角公式可得:
那么
扇形 CEF 的面积为
扇形 OEF 的面积为
三角形 EOC 的面积为
注意到三角形 EOC 和 三角形 FOC 是全等的:
那么我们要求的左上阴影面积为
从而阴影部分面积为
方法二:解析方法
如图,以圆心 O 为原点,OD 为轴正方向建立平面直角坐标系。根据图形对称性,我们依旧只需要求半边阴影部分面积即可。

容易得出半圆的方程为
弧 BD 的方程为
联立两个方程可解得 E、F 的坐标为
先计算半圆上的弧 EF 与轴所为的面积,如下图

令,则
那么也可以表示为
令,则
再计算下面的弧 EF 与轴所为的面积,如下图

令,则
那么也可以表示为
令,则
那么上面的阴影部分面积为
从而阴影部分面积为
,