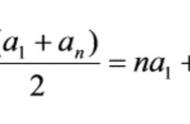等差数列求和公式
从高斯求和的故事还可以看出,等差数列求和的方法,是通过适当搭配,转化成若干个相等的数求和,即转化为乘法。
搭配的方法不是唯一的。一个等差数列除特殊情况外(每个数都相等的情况可直接用乘法),不是逐渐增大就是逐渐减小。如果是逐渐增大,调过头来写,就是逐渐减小。再把对应项相加,其和都相等,这样就可以转化成乘法。如
S=1+2+3+4+5+6+7+8+9+10 ①
S=10+9+8+7+6+5+4+3+2+1(加法交换律) ②
①十②得:
2S=11×10
S=(11×10)÷2=55
一般地,设 S=a1+(a1+d)+(a1+2d)+…+[a1+(n-3)d]+[a1+(n-2)d]+[a1+(n-1)d]
S=[a1+(n-1)d]+[a1+(n-2)d]+[a1+(n-3)d]+…+(a1+2d)+(a1+d)+a1
(上、下对应项的和都与“首项+末项”相等)则2S=(首项+末项)×n
S=(首项+末项)×项数n÷2
这就是等差数列前n项和的公式,即等差数列前n项和=(首项+末项)×项数÷2
如果项数是奇数,还可以用“中间项”乘项数,来求和。