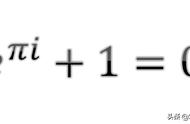作者 | 刘洋洲
来源 | 转自知乎专栏《万物皆数也》,“数学英才”获授权转载,在此感谢!
简介:皮克定理
图1:格点多边形
如图1,设网格边长为1,如何计算图中多边形面积?或许我们会考虑利用割补法来化简计算难度,甚至我们干脆使用勾股定理和余弦定理……但这都不是本文所要探讨的内容。以上例子中所探讨的问题,我们称之为求格点多边形的面积(格点多边形,即多边形顶点位于格点的多边形),我们有专门的计算公式,即——
皮克定理(Pick's Theorem)
其中是格点多边形内部的点的个数,我们简称为内点数,是格点多边形边界点的个数,我们简称为边界点数。
我们随后讨论该定理的证明。观察并欣赏此定理,有几个值得一提的事实:
格点多边形的面积只与内点和边界点的数量有关,和多边形具体的形状无关;
格点多边形的面积是0.5的整数倍。
皮克定理既实用又富有理论价值。我们不需要余弦定理,只需要简单的计数,就连小朋友都可以得知平面不规则图形的面积。更进一步,我们利用此公式逼近闭曲线围城的面积,从而得到近似值;直观上讲,若网格越是细密,近似值就越精确,这当中蕴含着微积分的思想。
铺垫:欧拉公式
图2:3个洞就是3亏格
使用平面图的欧拉公式证明相对来说比较简洁。刚好我在之前的文章中有证明过平面图的欧拉公式,感兴趣的读者可以阅读《从黄金多面体到欧拉特征》(点击文章题目查看)。我们顺便介绍一个更一般的公式——
可定向闭曲面的欧拉公式
其中,表示有个“洞”的可定向闭曲面,例如图1中的圆环面,它只有一个“洞”,即。“洞”我们有个专有名词——亏格,我们下文仅仅需要用到亏格为的情况。公式中分别表示曲面上剖分的顶点数、棱数、面数。如图3,就是对圆环面的剖分;足球,则是用五边形与六边形对球面剖分。可定向闭曲面欧拉公式揭示了欧拉特征与曲面亏格之间的关系,这是数与形的美妙联系。
图3:矩形剖分