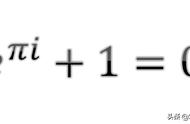家族式社会一度成为古代中国的发展潮流,家族的家谱也成为家族的重要部分,直到今天仍有许多家族保留家谱。在数学史的发展中也有这么一个家谱,它有顶级数学家组成,称它为“最豪华家谱”一点也不为过!
这个家谱要从莱布尼茨说起,莱布尼茨收了个学生叫约翰·伯努利,伯努利收了一个徒学生就是著名的欧拉,欧拉在他的那个时代是无敌的存在。然后欧拉收了一个学生叫拉格朗日,拉格朗日收了一个学生柯西,就是著名的柯西不等式的柯西。柯西收了个学生被称为“数学王子”的高斯,高斯有个徒弟叫黎曼,就是被称为“数学桂冠上的明珠”黎曼猜想,黎曼几何又成就了爱因斯坦的相对论。
莱布尼茨☞约翰·伯努利☞欧拉☞拉格朗日☞柯西☞高斯☞黎曼☞爱因斯坦(黎曼几何成就爱因斯坦相对论)。
这就是传承,不得不说莱布尼茨的这一支太豪华,太强大了!
下文我们简单的聊一聊这些顶级的数学家的成就:
①伟大数学家莱布尼茨,他是牛顿的一生死敌,与牛顿先后创立了微积分。1684年10月,莱布尼茨在《教师学报》上发表的论文《一种求极大极小的奇妙类型的计算》在数学史上被认为是最早发表的微积分文献。他还发明了一套符号系统,如引用dx表示x的微分,∫表示积分,dx表示n阶微分等等。这些符号进一步促进了微积分学的发展。1713年,莱布尼茨发表了《微积分的历史和起源》一文,总结了自己创立微积分学的思路,说明了自己成就的独立性。

②约翰·伯努利巧妙地利用了费马原理将力学问题变成了光学问题,通过械能守恒定律和斯涅尔定律解决了最速降线问题这一难题。他还成功地用微积分证明悬链线是一条双曲悬链函数。

③欧拉——数学史上第二高产的数学大师,他用欧拉公式将复数的指数函数与三角函数串联起来,而这个公式在x等于π时,就是我们常说的最美公式,也被物理顽童费曼先生成为“最卓越的数学公式”。1735年欧拉解决了长期悬而未决的贝塞尔问题,即所有正整数平方的倒数和是多少。这个问题在多年后被解析延长拓展为黎曼zeta公式,从而有了那个价值100万的黎曼猜想。

④拉格朗日在柏林工作的前十年,把大量时间花在代数方程和超越方程的解法上,作出了有价值的贡献,推动一代数学的发展。他提交给柏林科学院两篇著名的论文:《关于解数值方程》和《关于方程的代数解法的研究》 。把前人解三、四次代数方程的各种解法,总结为一套标准方法,即把方程化为第一次的方程(称辅助方程或预解式)以求解。近百余年来,数学领域的许多新成就都可以直接或间接地溯源于拉格朗日的工作。所以他在数学史上被认为是对分析数学的发展产生全面影响的数学家之一。