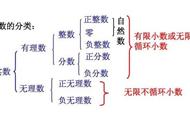
“i”的引入:方程x² 1=0,在实数范围内无解,为了解决类似问题,引入了一个新数“i”,使得x=i是方程x² 1=0的解,即i²=-1。
把实数b与i相乘,记为bi,
把实数a与bi相加,结果记为a bi。
所有实数以及i都可以写成a bi(a,b∈R)的形式,从而,这些数都在扩充后的新数集内(复数集)。
实数集R是复数集C的真子集,即R⫋C。
复数分为实数和虚数,复数a bi(a,b∈R),当b=0时,为实数;当b≠0时,为虚数,其中当a=0时,为纯虚数。
虚数单位i的乘方具有周期性,最小正周期为4。
i¹=i,i²=-1,i³=-i,i⁴=1……
进而推广得到
i⁴ⁿ⁺¹=i,i⁴ⁿ⁺²=-1,i⁴ⁿ⁺³=-i,i⁴ⁿ⁺⁴=1(n=0,1,……)
利用此周期性可快速解决有关i的乘方的计算问题。
例题:


另外,1 i/1-i =i, 1-i/1 i =-i最好也记住,不难推导,将分母实数化即可。
,