作者 | 刘瑞祥
来源 | 说短论长
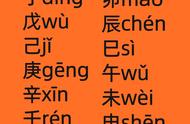
我在高中学完排列组合后曾经思考过这样一个问题:天干一共是10个字:甲乙丙丁戊己庚辛壬癸,地支是12个字:子丑寅卯辰巳午未申酉戌亥。那么按照排列的结果,一共有120种结合方式,但为什么60年一个甲子?

后来当然我是明白了,原因在于天干地支必须按顺序循环,不能随意结合。比如“甲子”“乙丑”等等是合法的,而“甲丑”“乙子”等等则是非法的。换言之,奇数位置的天干只能和奇数位置的地支结合,偶数位置的天干只能和偶数位置的地支结合。这里的道理在于,10和12的最大公约数是2,所以“合法”的结合方式必须是10和12的乘积除以2,即二者的最小公倍数。
下面我设计一种操作来帮助大家理解:取一些长度为10里面的纸张,每隔1厘米画一条线,然后每张纸都按顺序写上从甲到癸等天干字样,另外取一些长度12里面的纸,也是每隔1厘米画一条线,每张纸按顺序写上从子到亥等地支字样。然后两种纸分别首尾相接排成两排,显然6张代表天*纸长度和5张代表地支的纸相同。如果两种纸起点位置相同又朝一个方向铺排的话,那么可以看到:“甲”永远不可能和“丑”并排,“乙”永远不能和“子”并排,最后能出现的结合方式正好是60种。
下面这种操作是错误的:弄两个罐子,其中一个里作好10个阄,分别写上天干字样,另外一个里有12个写上地支字样的阄。每次分别从两个罐子里各抓一个结合在一起,然后放回再重新抓。这样一直操作下去并且把每次结果记录下来,显然有120种可能性。
我们还可以这样设想一下:如果天干只有2个(设为甲乙)而地支有4个(设为子丑寅卯),则合法的组合只有4种,决不可能是8(2乘4)种:即甲子、乙丑、甲寅、乙卯。但如果天干有3个而地支有4个,那么合法的组合就是12种了,恰好等于二者的乘积。类似的,如果天干有9个而地支有12个,则合法的结合方式只有36种,尽管9和12的乘积是108。
下面附上现实生活中全部合法的组合: