有这样一道题目,用1除以3,得到无限循环小数0.33333333...,可是这个无限循环小数乘以3的结果是无限循环小数0.99999999...却不等于1?
实际情况到底是怎么样呢?我们来看几个问题,发散一下思维:
什么是无限循环小数?
无限循环小数0.99999999...的分数表达式是什么?
1-0.99999999...=?
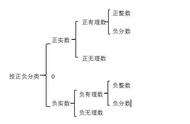
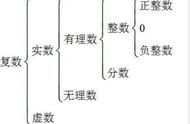
所有的实数分为两类:有理数,无理数
其中有理数就是所有能够表示为分数的数字,即像下面这个样子:

无限循环小数也是有理数,可以用分数形式表示,但无法分子除以分母无法除尽。比如本文中的无限循环小数0.33333333...就是1/3,但问题是0.99999999...的分数形式是什么???
1与0.99999999...的差是0
用a来表示1-0.99999999...,很显然a≥0。但是你任意找一个正数,a都比他小。比如不难验证
a<0.1,
a<0.01,
a<0.000000000000000000000000000001,小数点后面的0可以任意多。
本文不去叙述这个命题的严格证明,但是大家可以随意验证任意小的正数都比a大。另外,本文中所述无限循环小数可以表示为分数的形式,也不在此给出严格证明。以后有机会单独开一篇文,对这两个命题进行论述。
其实,绕了一圈,“0.333×3=0.999...不是1”就是一个关于无限循环小数表示形式的认知上的偏差,不算作数学悖论。