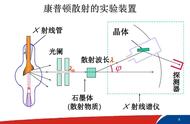
一、光的散射
由于光在介质中与物质微粒的相互作用,使光的传播方向发生改变的现象,叫做光的散射.
二、康普顿效应
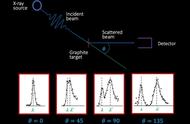
光可以与介质中的物质微粒发生散射,改变传播方向。1918~1922年,美国物理学家康普顿在研究石墨对X射线的散射时,发现在散射的X射线中,除了与入射波长相同的成分外,还有波长大于入的成分,这个现象称为康普顿效应(Compton's effect)。康普顿的学生,中国留学生吴有训测试了多种物质对X射线的散射,证实了该效应的普遍性。
按照经典物理学的理论,入射的电磁波引起物质内部带电微粒的受迫振动,振动着的带电微粒进而再次产生电磁波,并向四周辐射,这就是散射波。散射的X射线频率应该等于带电粒子受迫振动的频率,也就是入射X射线的频率。相应地,X射线的波长也不会在散射中发生变化。因此,康普顿效应无法用经典物理学解释。
康普顿用光子的模型成功地解释了这种效应。他的基本思想是:光子不仅具有能量,而且具有动量,光子的动量p与光的波长入和普朗克常量h有关。这三个量之间的关系式为:
①E=mc²
②E=hν
③p=mc
④ν=c/λ

在康普顿效应中,当入射的光子与晶体中的电子碰撞时,要把一部分动量转移给电子,因而,光子动量可能会变小(如图所示)。从p=h/λ式看,动量p减小,意味着波长变大,因此,这些光子散射后波长变大。

基于这个假定的理论结果与实验符合得很好。康普顿效应让人们对光子有了更深入的认识。康普顿因此获得了1927年的诺贝尔物理学奖。
例题:频率为ν的光子,具有的能量为hν,动量为hν/c,将这个光子打在处于静止状态的电子上,光子将偏离原运动方向,这种现象称为光子的散射,下列关于光子散射的说法正确的是(A)
A.光子的运动方向改变,但传播速度大小不变
☞光子质量减小
B.光子由于在与电子碰撞中获得能量,因而频率增大.
C.由于受到电子碰撞,散射后的光子波长小于入射光子的波长
D.由于受到电子碰撞,散射后的光子频率大于人射光子的频率
☞1.在光的散射中,光子不仅具有能量,也具有动量,在与其他微粒作用过程中遵守能量守恒定律和动量守恒定律;
2.光电效应和康普顿效应都说明光具有粒子性。
三、光的波粒二象性
众所周知,在麦克斯韦的电磁理论建立之后,人们认识到光是一种电磁波,从而光的波动说被普遍接受,人们不再认为光是由粒子组成的。而爱因斯坦的光电效应理论和康普顿效应理论表明,光在某些方面确实会表现得像是由一些粒子(即一个个有确定能量和动量的“光子”)组成的。也就是说,光电效应和康普顿效应重新揭示了光的粒子性。当然,此时人们对光的粒子性的认识,是以最新的实验和量子理论为基础的,已经和牛顿时代的光的粒子说根本不同,其深度远远超出后者。人们意识到,光既具有波动性,又具有粒子性。换句话说,光具有波粒二象性(wave-particle dualism)。此后,又经过一系列探索,人们最终建立了比较完善的,能统一描述光的波动性和粒子性的理论一量子电动力学。
从牛顿时代光的微粒说、惠更斯和托马斯·杨的光的波动说,到麦克斯韦的光的电磁理论,再到爱因斯坦的光子理论乃至量子电动力学,人类对光的认识构成了一部科学史诗。
【问题】
例题1.在光电效应实验中,如果入射光的波长确定而强度增加,将产生什么结果?如果入射光的频率增加,将产生什么结果?
【答案】
光强增加有三种情况:
1.光子数目增加;
2.光的频率增加大;
3.光子数目增加和光的频率增大。
如果入射光的波长确定而强度增加(光子数目增加),将分为以下两种情况:
1.入射光的波长较长(频率较短),以至于光子的能量较低,无法激发出电子。这时候即使强度增加,光电效应同样不会发生;
2.入射光的波长较短,光子的能量较高,可以激发出电子。这时候强度增加,即单位时间内入射光的光子数增加,从而激发出更多的电子,所以促进光电效应,光电流增加。
光电流I=nqsv(n为光电子数密度)
如果入射光的频率增加(光子数目不变),将分为以下两种情况:
1.入射光刚开始时的频率较小,当入射光的频率增加,刚开始可能无法激发光电子,当入射光频率达到一定程度后激发出光电子,且发射的光电子最大初动能增加;
2.入射光刚开始时的频率较大,入射光的频率增加,发射的光电子最大初动能增加,光电流也增大。
例题2.金属A在一束绿光照射下恰能发生光电效应,现用紫光或红光照射时,能否发生光电效应?紫光照射A、B两种金属都能发生光电效应时,为什么逸出金属表面的光电子的最大速度大小不同?
【答案】:光电效应的条件是入射光的频率大于或等于金属的极限频率,才能发生光电效应,在一束绿光照射下恰能发生光电效应,由于紫光频率大于绿光频率,则现用紫光照射时,一定发生光电效应;由于红光的频率小于绿光频率,则现用红光照射时,一定不发生光电效应;根据光电效应方程知,Ekm=hν-W₀,紫光照射A、B两种金属都能发生光电效应,最大初动能与金属的逸出功有关。
例题3.铝的逸出功是4.2eV,现在将波长为200nm的光照射铝的表面。
(1)求光电子的最大初动能。
(2)求截止电压。
(3)求铝的截止频率。

例题4.根据如图所示

的电路,利用能够产生光电效应的两种(或多种)频率已知的光来进行实验,怎样测出普朗克常量?根据实验现象说明实验步骤和应该测量的物理量,写出根据本实验计算普朗克常量的关系式。

例题5.在日常生活中,我们不会注意到光是由光子构成的,这是因为普朗克常量很小,每个光子的能量很小,而我们观察到的光学现象中涉及大量的光子。如果白炽灯消耗的电功率有15%产生可见光,试估算60W的白炽灯泡1s内发出可见光光子数的数量级。