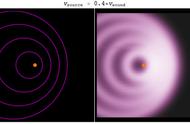
多普勒效应 Doppler effect

观察者与波源之间有相对运动时,观察者测得的频率与波源的振动频率不同的现象。奥地利物理学家J.C.多普勒在1842年发表的论文中开始研究这一现象。
声波和电磁波(包括光波)的传播中都有类似的现象。声波的传播以介质为载体,不同介质中声波速度不同,且和介质的运动有关,但它不能在真空中传播;而电磁波(包括光波)的传播不需要介质为载体,且从任一惯性参照系来观测真空中的光速相同。
由于以上差别,声波和光波的多普勒效应所遵守的规律是有区别的。
1.声波多普勒效应
与以下因素有关:
1.1.声源运动时介质质元的振动频率
静止的介质中声波的传播速度是由介质的特性决定的,波长和介质质元的振动频率之间有以下关系:
(1)
式中是与波源的频率有关的,如果的运动速度,则;如果作直线运动,则在的前方介质中的波长将被“挤短”。从上式可判断,介质质元的振动频率将变大;令的振动周期为,则波长被“挤短”的距离为,因而波长将为:
(2)
将(2)代入(1)可得:
(3)
上式说明在波源的前方。如果在波源的前方放一个接收器,则收到的也是介质的振动频率,而不是波源的频率。
为了以下讨论方便,可把坐标定在地面,定义从到的方向为正方向,即当向运动时,当离开运动时。
当时,(2)式和(3)式中的改变为负数,这相当于(2)式中的波长被“拉长”,从(3)式看介质的振动频率将变低,即。
当的运动速度超过介质中的波速度时(即),就会在介质中产生激波,并成为流体中的主要声场。的前方,在到达前其本身的振动不会影响其前方的介质。
1.2.接收器运动时收到的频率
进入介质中的波,(1)式中的频率和波长不再受声源的影响。此时介质的振动要用一个接收器(人耳也是声波接收器)来探测。
以表示的运动速度,沿用以上定义的坐标,当接收器向着波源运动时,为负数;但接收器离开波源运动时,为正数。
当,收到的频率。
当时,将迎着传来波去接受介质振动,每秒接收的振动次数增加量为;而当时,将逃离传来波并使接收到的振动次数使减少,每秒接收的振动次数将减少。
从以上分析,和的关系可以表示为:
(4)
1.3.波源和接收器都运动时接收器收到的频率
(3)式代表的运动时介质的振动频率和波源的频率的关系,把(3)中的代入(4),即可得到波源和接收器都运动时接收器收到的频率:
(5)
1.4.介质运动的影响
声波是以介质为载体的,介质的运动相当于改变波的运动速度,沿着介质的运动方向声波传播得快,逆着介质的运动方向声波传播得慢。
设介质的运动沿着和的连线方向,速度的大小为,则和的关系如下:
(6)
从上式不难看出,当同时有和时,波源和接收器之间距离不变,这时接收器收到的频率和波源的频率相同,和无关。
如果观察者和波源以及介质的运动不在一条直线上,则上式中的、和分别表示它们在和的连线上的投影。
2.电磁波多普勒效应
声波的传播是要以介质为载体的,而电磁波(包括光波)的传播不需要介质为载体。
从任一惯性参照系(如波源或接收器)来观测,电磁波在真空中的传播速度相同。因此,电磁波的多普勒效应的公式,要根据狭义相对论中的洛伦兹变换求出:
(7)
式中和分别表示波源S和接收器R的频率,是真空中的光速。现以代表波源的位置,代表接收器R的位置,公式中和是以观测者为参照系来表述的,波源的速度是矢量,是它的数值,也是矢量,是和之间的夹角。
与声波的多普勒效应不同,电磁波的多普勒效应有以下特点:
①虽然参照系选在接收器R上,而R也是以一定速度运动的,物理上(7)中只有S和R间的相对关系,即矢量和。
②当和垂直时,,这时仍然有多普勒效应,叫作横向多普勒效应;声波的传播中没有横向多普勒效应。当和同向或反向时,叫作纵向多普勒效应。
3.多普勒效应的实例和应用

多普勒效应的应用:超声心动图
日常生活中,在铁路边经历火车通过时,听到的汽笛声是变化的:只有火车到达的瞬间听到的是汽笛的原始振动频率,不火车开来时听到的频率大于,火车离开时听到的频率小于。早期的对多普勒效应的实验验证,也是把声源放在车子上进行的。
天文学上从双星的光谱的周期性变化,可测出它们的运动情况。天文学家出恒星的光谱向低频方向移动(称为红移),根据多普勒效应的原理可求出这些天体离开地球的速度,这已成为现代宇宙学的实验基础。发光的原子的无规热运动会使光谱谱线增宽。
多普勒效应可用于测量运动物体的速度,物体既可是自身能发出波的,也可是反射波的,前者称为主动量,后者称为被动测量。
从汽车、火车等交通工具,到水上和水下目标,液体中的颗粒以及红细胞等,都可利用多普勒效应的原理测量其运动速度。有的已成为商品仪器,如医用的超声波多普勒血流仪、民用或警用的雷达测速仪等。
推荐书目
爱因斯坦 A. 相对性原理. 北京:科学出版社1980.
EINSTEIN A, LORENTZ A, MIKOWASKI H, WEYL H. The Principle of Relativity. New York: Dover Publications, 1923.
摘自:《中国大百科全书(第2版)》第5册,中国大百科全书出版社,2009年
,