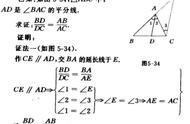
在学习角平分线的轴对称之前,学习了全等三角形,因此很多同学都习惯性地利用全等三角形解题,不知道如何正确使用角平分线的性质定理或判定定理进行解题。本篇主要介绍角平分线的基本定义,角平分线的性质与角平分线的判定,学会用数学语言进行证明,而不是所有的题目都依靠全等三角形。

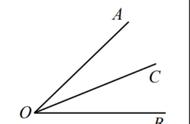
角平分线的定义,相信大家都不陌生,从一个角的顶点引出一条射线(线在角内),把这个角分成两个完全相同的角,这条射线叫做这个角的角平分线。在定义中,已知角平分线,得到两个角相等,即“知一推一”,知道一个条件,推出一个结论。

通过角平分线的基本概念,可以得到两个角的数量关系,两个角相等,或者小角是大角的一半,或者大角是小角的两倍。
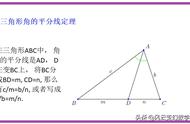
角平分线的性质定理:知三推一角平分线的概念基本不会出错,但是很多同学不会使用角平分线的性质定理与判定定理。角平分线的性质定理:角平分线上的点到角两边的距离相等。这句话中有两个重点:(1)角平分线上的点;(2)距离,得到的结论是相等。

由1个角平分线 2个垂直得到线段相等,三个条件缺一不可。并且要注意的是,由角平分线的性质定理不能直接得到线段OA=OB,如果要得到这个结论,需要证明△PAO≌△PBO。