角平分线定理及其证明

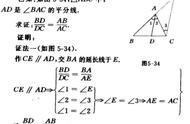
在三角形中有一个角平分线定理,说的是:在三角形ABC中, 角A的平分线是AD, D在变BC上, 将BC分成BD=m, CD=n, 那么有c/m=b/n, 或者写成c/b=m/n. 该定理的逆定理也是成立的。
如果将这个定理与斯图尔特定理结合起来,可以求出角的平分线的距离:

关于斯图尔特定理的证明,请参见头条的另一篇文章,。

现在我们证明三角形角平分线的定理。
在三角形ABD和ACD中利用正弦定理有:

因为AD是角BAC的角平分线, 所以有∠BAD=∠CAD,
这样分母中的sin(BAD)=sin(CAD),
此外∠BDA ∠CDA=180°
因此有:
Sin(BDA)=Sin(CDA)
也就是上述的等式分子也相等,
因此:

有关角的平分线长度公式,读者根据斯图尔特公式可以用mb=cn替换后,提取公因式并约掉m n, 即可以证明。
有关角平分线的逆定理的证明,可以用假定法证明,即D点不是角分线上的点,那么一定存在另一个点D’ 是角分线上的点, 然后根据比例关系的唯一性,由此证明D与D’重合,由此证得逆定理成立。
,