一道初中几何题-求三角形的中线长
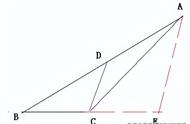
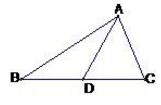
在图中, 三角形ABC是个直角三角形,∠BCA=90°, 中线CM垂直于中线BN, 若边长BC=s, 那么BN的长度是多少。

解:如图,设CM与BN的交点为P,那么在三角形CAN中有两个直角三角形都与直角三角形BCN相似。

本题将要用到两个定理:
- 射影定理。
- 形心将中线分割成2:1的定理。
由于M和N都是相应的边长BC和AC的中点,因此P是形心,因此有BP/PN=2:1,
设BN=x, 那么BP=2x/3,
射影定理成立是因为三角形BPC相似于三角形BCN,所以有:

带入相应的代数式有: