一道高中几何题-求三角形的中线
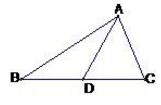
三角形ABC中,BC = √2, CA = 6,角ACB = 135°。如果CD是
AB的中点,求CD的长度是多少?
解:
方法1:三角法
如图做AE平行于中线CD, 延长BC与AE相交于E,

显然CD=AE/2, 现在求出AE就求出了CD,
但在三角形ACE中,有CE=BC=√2, CA=6,∠ACE=45°,
根据余弦定理:
AE2=62 2-2·6·√2·cos45°

由此得AE=√26
所以中线CD=(√26)/2
方法2:解析法
将点B置于原点,C点的坐标为(√2, 0)A点的坐标则为(4√2, 3√2)
那么AB中点的坐标为D(2√2, (3√2)/2), 根据两点之间的距离公式CD的长度为:

方法三:本题的另一种解法,是利用一个定理,这个定理被称作斯图尔特定理,其证明方法参见。
这个公式要求知道三角形的三个边,然后套用公式即可以求出中线的长度。
首先用余弦定理求出135°所对应的边为5√2, 然后即可求出结果。
这里省略。
,