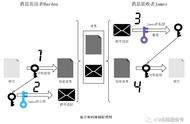
在公钥密码体制中,每一个用户都拥有一对个人密钥k=pk,sk),其中pk是公开的,任何用户都可以知道,sk是保密的,只有拥有者本人知道。假如Alice要把消息m保密地发送给Bob,则Alice利用Bob的公钥pk加密明文m,得到密文c=E(pk, m),并把密文传送给Bob。Bob得到Alice传过来的c后,利用自己的私钥sk解密密文c得到明文m=D(sk,c)。
公钥密码体制与对称密码体制的主要区别是前者的加密密钥和解密密钥是不同的。这个不同导致了:①在公钥密码系统中,密钥维护总量大大减少;②在公钥密码系统中可以很容易实现抗否认性。

1. RSA公钥密码体制
RSA密码体制是世界上应用最为广泛的公钥密码体制。RSA体制的安全性基于大整数分解的困难性,即已知两个大素数p和q,求n=pq是容易的,而由n求p和q则是困难的。
RSA算法包括密钥生成算法和加解密算法两部分。
RSA密钥生成算法如下:
①选择不同的大素数p和q,要保密,计算n=p∙q,将n公开,
φ(n)=(p-1)(q-1),φ(n)要保密。
②选择e,满足1<e<φ(n),且gcd(φ(n),e)=1,(n,e)作为公钥,将e公开。
③通过计算ed ≡ 1 mod φ(n),且e≠d,d≡^(−1) mod φ(n),(n,d)作为私钥,d要保密。
RSA加解密算法如下:
加密运算c≡^ (mod n),解密运算m≡^ (mod n)。
加密时首先对明文比特串分组,使得每个分组对应的十进制数小于n,即分组长度小于n。
例3-1 取素数p=101,q=113,则
n = p∗q = 101×113 = 11413
φ(n) = (p-1)(q-1) = 100×112 = 11200
选择e=3533,验证gcd(e,φ(n)) = gcd(3533,11200) = 1
则d ≡ ^(−1) mod φ(n) = 〖3533〗^(−1) mod φ(n) = 6597
公钥(n, e) = (11413, 3533)
私钥(n, d) = (11413, 6597)
加入要加密的明文为m=9276,则密文为
c ≡ ^ (mod n) = 〖9276〗^3533 (mod 11413) = 5761
接收方用私钥解密明文得
m ≡ ^ (mod n) = 〖5761〗^6597 (mod 11413) = 9726
(mod 11413) = (mod 11413)
(mod 11413) = (mod 11413)
= (mod 11413)
= 4053 * 144 (mod 11413)
= 1569 (mod 11413)
(mod 11413) = 9276*1569 (mod 11413)
= 2469
gcd(3533,11200)
11200=3533*3 601
3533=601*5 528
601=528*1 73
528=73*7 17
73=17*4 5
17=5*3 2
5=2*2 1
2=2*1 0
1=5-2*2
=5-(17-5*3)*2
=5*7-17*2
=(73-17*4)*7-17*2
=73*7-17*30
=73*7-(528-73*7)*30
=-528*30 73*217
=-528*30 (601-528)*217
=601*217-528*247
=601*217-(3533-601*5)*247
=601*1452-3533*247
=(11200-3533*3)*1452-3533*247
1=11200*1452-3533*4603
1 mod 11200 = -3533 * 4603 mod 11200
mod 11200 = -4603
( 11200 ) mod 11200 = 6597
mod 11200 = 6597
中国剩余定理
a=288, b=158,gcd(288,158)
xa yb=gcd(a,b)
288=158*1 130
158=130*1 28
130=28*4 18
28=18*1 10
18=10*1 8
10=8*1 2
8=4*2 0
gcd(288,158)=2
a=288, b=158,gcd(288,158)
xa yb=gcd(a,b), gcd(288,158)=2
2=10-8*1
=10-(18-10)
=10*2-18
=(28-18)*2-18
=28*2-18*3
=28*2-(130-28*4)*3
=28*14-130*3
=(158-130)*14-(288-158)*3
=(158-288 158)*14-(288-158)*3
=158*28-288*14-288*3 158*3
=-17*288 31*158
ed ≡ 1 mod f
d ≡ mod f
mod 1769
1769=550*3 119
550=119*4 74
119=74*1 45
74=45*1 29
45=29*1 16
29=16*1 13
16=13*1 3
13=3*4 1
3=1*3 0
Gcd(1769,550)=1
1=13-3*4
=13-(16-13)*4
=13*5-16*4
=(29-16)*5-16*4
=29*5-16*9
=29*5-(45-29)*9
=29*14-45*9
=(74-45)*14-45*9
=74*14-45*23
=74*14-(119-74)*23
=74*37-119*23
=(550-119*4)*37-119*23
=550*37-119*171
=550*37-(1769-550*3)*171
1=550*550-1769*171, x=550, y=-171
1 mod 1769 = (550*550) mod 1769
mod 1769=550
简单例子
mod 13
mod 13 = 4
mod 13 = 16 mod 13 = 3
mod 13 = (11* * ) mod 13
= (11*4*3) mod 13
= 2


@木子雨辰,将一直带给大家信息安全知识,由浅至深、采用体系化结构逐步分享,大家有什么建议和问题,可以及留言,多谢大家点击关注、转发,谢谢大家。
,