这个问题提的很好,高中时学习了圆周运动公式和万有引力定律后,也产生了相同的疑问。后来看了一些卫星的发射和轨道设计,逐渐也就明白了。
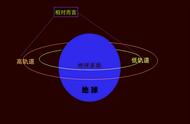
根据万有引力定律和向心力公式得出卫星的运动速度Ⅴ=√(GM/r),其中G为万有引力常数,M为地球质量,r为卫星距地心距离。卫星的确是在低轨运动速度快,高轨运动速度慢。但这里面有两个问题:
第一,高轨道速度是慢,但前提是必须到那里,到那里才能慢。怎么到那里?卫星在各自轨道运动,不可能无缘无故到别的轨道,这需要一个变化过程,尤其是受重力影响,需克服重力做功才能抬高轨道。所以说这个低轨变高轨加速只是一个过程,不是最终目的。当然这个变化过程有很多种方法,加速只是其中最常用的方法,下面会讲到为什么要用这个方法。
第二,低轨运动速度快,高轨慢。这只是指正圆形轨道,而卫星和所有行星一样,都遵从开普勒第一定律,即绕地球的运转轨道几乎都是以地球为其中一个焦点的椭圆轨道。椭圆轨道就比较复杂了。拿地球来说吧,第一宇宙速度是7.9千米/秒,理论上这是地球表面(最低轨道)的环绕(圆形轨道)速度,也是卫星环绕地球(圆形轨道)的最大速度。任何高于地面的圆形轨道的速度都低于这个速度。但近地的椭圆轨道,它们大部分轨道的速度却大于7.9千米/秒,并且速度越大(只要小于11.2千米/秒的速度,卫星就不会逃离地球),

椭圆偏心率越大,远地点轨道高度越大。所以从这个意义上来说,想获得高轨道应该加速。这也是科技人员抬高卫星轨道的常用方法,下面咱们详细讨论一下。
咱们先来分析一下卫星运行在椭圆轨道的能量变化。由于卫星只受到重力的作用,因此它遵守机械能守恒定律。也就是说卫星在椭圆轨道的远地点虽然重力势能最大,但它的动能最小,即运动速度最小。而在近地点势能最小,但动能最大,卫星的运动速度最大。也就是说近地点的速度是大于与近地点轨道高度相同的圆形轨道或其它小椭圆轨道的运动速度的,因此人们常采用在近地点(或圆形轨道的任一点)加速的方式来获得大椭圆轨道,然后再在高轨道适当调整速度就可达到提升轨道的目的。为了节省燃料,最后一般选择在远地点提速进入高轨道的圆形轨道(这叫圆化轨道),或者进入更大的椭圆轨道。我国发射月球探测器的地月转移轨道说到底就是在近地点不断加速,得到的远地点40多万公里的大椭圆轨道,最终在靠近月球时被月球引力捕获。

以上是人们常采用加速进入大椭圆轨道来达到提升轨道高度的方法。当然还有别的方法,比如说卫星燃料充足,携带的推进器动力强劲,我很任性,利用平行四边形法则,就可以调整卫星运动方向直接升轨,就像火箭的发射段,只要克服重力作功直接上升,到达目的地后直接减速到这个高度应有的速度即可,你看不但不加速,还减速。但这种方法太浪费了,消耗能量大,人们很少选择。
对于降轨当然也有很多方法,这要根据不同的降轨要求来决定。一种是从大椭圆轨道降低到小椭圆轨道或以近地点高度圆化轨道。这时一般采用在近地点制动减速,这种降轨是近地点高度不变,因为近地点卫星的运动速度大于同等高度圆形轨道的运动速度。这样远地点轨道高度就降下来了,轨道变圆了,相比之下远地点降轨后的速度增加了。另一种是降低近地点高度。这时一般采用卫星直接制动减速调向,卫星高度受重力影响下降。虽然卫星高轨势能大于低轨,但卫星所受重力刚好用于卫星做圆周运动的向心力,如果不减速降低向心力,将没有多余的重力做功把势能转化为动能,也不会降低卫星轨道,卫星的运动方向也不会改变,所以降轨要减速调向,不过这只是一个过程。降到目标高度后运动速度也调整到这个高度应有的速度,这个速度调整一般是加速。当然我很任性,利用平行四边形法则,我就要用轨控发动机直接向上喷气反冲向下合力加速降轨到目标高度也可以。
总之,卫星低轨变高轨,一般在近地点加速后再把远地点速度加到相应速度。而高轨变低轨,一般在近地点制动减速到达目的地后再加速。至于高轨和低轨的能量比较,在地球有效引力范围内当然是高轨卫星具有的机械能大,但为了变轨,无论是升轨还是降轨,这个过程都需消耗能量,说的是过程。
轨道设计本身就是一个复杂的工程,美国人的轨道设计技术炉火纯青,可以连续利用行星引力加速变向,设计运动周期可以长达几十年,太阳系各大行星的相对位置一直变化,但他们对每个时间和位置节点算计精准,既满足任务要求,又能拓展设计,这种水平令人叹为观止。

美国“旅行者2号”四十年轨道运行图

目前进入太阳系外缘星际空间的人类探测器
咱们今天只为抛砖引玉,作一简单科普,有兴趣的朋友可以深入研究。
,