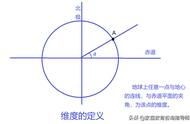
如上图:在桩位中心O1安平仪器,当望远镜视线水平时(镜筒处于90°0′0″或270°0′0″),视线OM和视距尺垂直相交于M点,从望远镜内上下视距线a、b出发的平行光线,经物镜折射后,经过物镜生焦点F与视距尺相遇于A、B两点,两点间距离R叫做视距,尺离仪器越远,R值就越大,反之就越小,根据R值和几何关系即可算出仪器中心O到尺间的水平距离D;
同时在望远镜镜筒中丝在视距尺M点的读数即为仪器高度。

竖直角的识读计算

在桩位中心O1安平仪器,当望远镜视线水平后(镜筒处于90°0′0″或270°0′0″),转动望远镜镜筒瞄准目标得到一个角度为α,则找正目标后的竖直θ为:
当左盘时:θ=90°—α;
当右盘时:θ=α-270°;
水平视距的计算:
望远镜分划板上有上、下两短线,它与标尺配合,可以求得测站点到标尺之间的距离。
D=KR C式中:
D——目标到测站点的距离(m);
R——上下视距丝在标尺上所截长度(m)
K——视距乘常数,K=100;
C——视距加常数,C=0。
2、视准轴倾斜时视距测量:

如图所示:在倾斜地面上进行规距测量,视线OM不能垂直尺面,而和水平线OG开成垂直角θ,不能使用视准轴水平时计算公式,要求水平距离D,就必须进行以下两步推导:
(1)从不垂直于尺面的视距AB求出垂直于尺面的Aˊ、Bˊ求出斜距离OM。
AˊBˊ= A B cosθ= R cosθOM = KRcosθ C(2)从斜距离OM求出水平距离D
D = OM×cosθ =(KRcosθ C)×cosθ =KRcos2θ Ccosθ内对光望远镜,式中Ccosθ可以省略,水平 距离计算公式为:
D = KRcos2θ式中:
D——O1和P之间水平距离;
R——望远镜内两视距丝所截得的长度;
K——望远镜的视距常数,K=100;
θ——倾斜视准轴线和水平线间竖直角。
7 线路高差测量
1、视准轴水平时高差及高程的测量: