* 本文获授权转载自上海《数学教学》2019年第2期。
IMMC 2017中华赛区命题A及其解法摘要
台北市立中山女子高级中学
上海中学国际部

注1:台北市立中山女子高级中学参赛队员为陈芊如、涂瑾瑜、陈品儒、王宣茹和林敬家,指导老师为林淑娥、洪瑞英、吴汀菱和李昌泽。
注2:上海中学国际部参赛队员为黄婷、金子意、蒋诺亚和郭雨珂,指导老师为张明欣。
《数学教学》编者按:
国际数学建模挑战赛IMMC (International Mathematical modeling chaiienge)是一项面向中学生的国际性数学建模竞赛。台北市立中山女子高级中学和上海中学国际部都组队参加了IMMC 2017中华赛区的比赛,取得了较好的成绩。为了使广大中学数学教师了解IMMC的试题及其解题特点,编者将上述两所中学对IMMC 2017的命题A(中华赛区)的解答情况作简单介绍。
1 命题A“通过卫星遥感技术测量地球”简介
1.1 背景
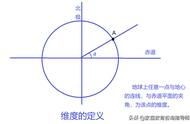
地球是人类赖以生存的家园,对其形状和各种物理现象的精细化认识一直是人们追求的目标。众所周知,地球形状近似椭球体,但其表面实际是一个凹凸不平的不规则体,有海洋、高山、平原、丘陵、沙漠等。精确测量地球的真实形状和大小是卫星遥感技术的主要应用方向之一。
1.2 说明
根据开普勒定律,卫星是在一个围绕地球的椭圆轨道上运动,这个椭圆轨道可以用六个轨道要素(也叫轨道根数)描述。如图1所示,以不转动地心赤道坐标系XYZ为参考,六个轨道要素是:半长轴, 偏心率e,轨道倾角i,近地角点距ω,升交点赤经Ω,过近地点时刻τ。轨道上的卫星位置可以用这六个参数确定。
(1) 轨道倾角i : 卫星轨道平面与地球赤道平面之间的夹角。
(2) 半长轴: 确定轨道大小的参数。圆轨道而言,就是圆的半径;对于椭圆轨道而言,就是椭圆的半长轴。
(3) 偏心率e: 确定轨道形状的参数。当e = 0时,轨道为圆,当0 < e < 1时,轨道为椭圆。
(4) 升交点赤经Ω: 确定轨道平面在空间位置的参数,沿着赤道方向,春分点至升交点(卫星由南半球至北半球穿过赤道平面的点)之间的角度。
(5) 过近地点时刻τ : 卫星运行中通过近地点的时刻。
(6) 近地角点距ω: 沿着卫星运动的方向,从轨道升交点度量至近心点的角度,也就是交点线与近地点矢径延长线之间的夹角。