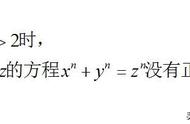大约在 1637 年左右,法国数学家费马在阅读丢番图(Diophatus)《算术》拉丁文译本
时,曾在第 11 卷第 8 命题旁写道:“将一个立方数分成两个立方数之和,或一个四次幂分成
两个四次幂之和,或者一般地将一个高于二次的幂分成两个同次幂之和,这是不可能的。关
于此,我确信已发现了一种美妙的证法,可惜这里空白的地方太小,写不下。”[1]
形如 = 的三元高次不定方程,在n > 2时永远没有(非平凡)整数解,这就
是费尔马大定理[2]。数学家费马当时留下了 n 为偶数的证明。如果再能证明 n 为任意奇素数
p 的形式,则整个证明就完全充足了。但这时可分两种情形:通常人们将p ∤ xyz叫做费尔马
大定理的第一情形;而把p|叫做费尔马大定理的第二情形。1998 年,作者给出了费马大
定理第一情形的初等证明[3]。本文给出费马大定理第二情形的初等证明。
当n > 2时,对于特定的p|,如果 = 有(非平凡)正整数解,则有p|和
p|两大类型。对于第一类型p|,本文仅证明p|这一情况,而p|情况与p|情况的证明类
似,故省略。为了字母处理方便,不妨把有p|和p|两大类型分别表示为下面两个不定方
程式:





完整课程 https://www.ixigua.com/6867412574724424204/
https://www.ixigua.com/6868164032307102215/
https://www.ixigua.com/6868512341680620035/
,