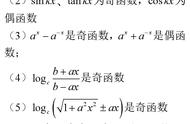对于函数f(x)的定义域内任意一点x,有f(x)=f(-x),则f(x)为偶函数;
对于函数f(x)的定义域内任意一点x,有-f(x)=f(-x),则f(x)为奇函数。
2,函数奇偶性的图像特征。(1)奇函数关于原点中心对称。
(2)偶函数关于y轴轴对称。
无论是关于坐标原点对称也好,还是关于y轴对称也罢,在x轴上都是关于0点对称的。
因此,函数判定奇偶性的大前提是定义域首先要关于0对称,否则就是非奇非偶函数。
(3)奇函数在关于原点对称的区间上具有相同的单调性。
(4)偶函数在关于原点对称的区间上具有相反的单调性。
3,函数奇偶性的判定:首先大前提,定义域关于0对称。
(1)定义法:将函数解析式中的所有x全部换成-x然后整理,如果整理之后的函数解析式与没换之前的函数解析式完全一致,则为偶函数;如果整理之后的函数解析式与没换之前的函数解析式恰好为相反数关系,则为奇函数;如果整理之后的函数解析式与没换之前的函数解析式既不相同又不相反,则为非奇非偶函数。
定义法是唯一大题写过程可用的方法。
(2)图像法:画出图像,看图像反映的定义域与对称性。
(3)特殊值法:做填空、选择题可用的简便方法,当然还是强调,试出来错的一定是错的,试出来是对的不一定是对的,最好能提前判断出是否可以试出对错。
奇偶性的试法是给x代入两个互为相反数的数(一般为1和-1,因为这两个数最好算),计算y值,若y值相等,则为偶函数;若y值为相反数,则为奇函数;若y值既不相等又不为相反数,则为非奇非偶函数。
特别注意,如果代入的相反数计算结果都为0,则无法判定奇偶性,因为0的相反数还是它本身,无法判定所得结果是相等关系还是相反数关系,需要换另一组相反数再试。
(4)特殊性质法:
奇 奇=奇;偶 偶=偶;奇-奇=奇;偶-偶=偶;
奇*奇=偶;偶*偶=偶;奇*偶=奇。
和上一节判定单调性一样,该方法有印象即可,不影响是否能做出题来,只影响做题速度。
4,分段函数奇偶性:只要是与奇偶性有关的分段函数题,一定是以0为分段点分为两段的。
我们常见的题型是,给出其中一段的解析式,告诉奇偶性,让写出另一段的解析式。
做法其实很简单:如果是偶函数,把给出段所有的x全部换成-x即为另一段的解析式;
如果是奇函数,把给出段的所有x全部换位-x,然后整体的相反数即为另一段的解析式。
5,复合函数奇偶性:复合函数奇偶性的判定有个心法口诀:
内偶外偶为偶,内奇外奇为奇,内偶外奇为偶,内奇外偶为偶。
这个心法口诀也是有印象即可,复合函数奇偶性的判定与普通函数一致。
6,为何叫奇偶性?我们一直强调,数学的概念可以用语文直译的方式理解。
但是这节说的奇偶性说到这,似乎和奇偶二字没有产生什么联系,这个性质的名字是随便起的吗?
当然不是。
那么奇偶性和奇偶二字有何关系呢?
比如:

我就可以直接说它是个偶函数。
再比如:

我就可以直接说它是个奇函数。
为什么?
上面解析式的x次数全部为偶次,它就是个偶函数;
下面解析式的x次数全部为奇次,它就是个奇函数。
这就是奇偶性与奇偶二字的联系。
下面我们做下变形,给上面两个式子后面都加一个数字。

偶函数增加一个数字,还是偶函数。

奇函数增加一个数字,就变成了非奇非偶函数了。
为什么?
增加一个数字,相当于增加了一个x的0次幂。
2002年新版数学国家标准中规定,0为偶数。
因此,偶函数增加一个数字,相当于x的次数还是均为偶次,所以依旧是个偶函数;
而奇函数增加一个数字,相当于x的次数既有奇次的又有偶次的了,所以成了非奇非偶函数。
奇偶性的这个特点常被用来考含参数的填空题。
7,一些常见的奇偶性函数:了解可以增加做题速度。

以上就是函数奇偶性的全部内容了,下节课我们讲函数周期性和对称性。
大家如果喜欢或者需要这份高中数学学习资料,别忘了点赞关注,我会以最简单明了的方式给大家讲解高中数学,帮助需要的高中生拿个好成绩。
,