一.概念描述
现代数学:一组对边平行而另一组对边不平行的凸四边形称为梯形,它是特殊的四边形之一。
小学数学:2004年人教版四年级上册教材第71页是这样定义的:只有一组对边平行的四边形叫作梯形。
二.概念解读
梯形是从哪里起源的呢?我国古算书中称梯形田为邪田,因此梯形图形也称邪田。
梯形在生活中的原型是什么?生活中的梯子、水渠的横截面、汽车的前挡风玻璃、跳箱的侧面等都是梯形的。
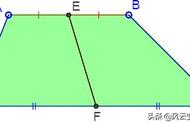
梯形有哪些特性呢?如下图:

四边形ABCD中,若AD∥BC,AB与CD不平行,则四边形ABCD是梯形。平行的两边AD、BC叫作梯形的底边,它们必不相等。其中长边BC叫下底,短边AD叫上底;也可以单纯地认为上面的一条叫上底,下面一条叫下底。不平行的两边AB、CD分别称为梯形的腰;上底与腰的夹角称为上底角,下底与腰的夹角称为下底角,并统称为梯形的底角。两底之间的距离称为梯形的高。梯形两腰中点的连线称为梯形的中位线,梯形的中位线平行于底边,并通过两对角线中点,且等于两底之和的一半。梯形两对角线的中点连线平行于底边,且等于两底之差的一半。
梯形的本质特征是只有一组对边平行的四边形,可分为一般梯形和特殊梯形。特殊梯形包括等腰梯形和直角梯形。其中,两腰相等的梯形叫等腰梯形;有一个角是直角的梯形叫直角梯形。
三.教学建议
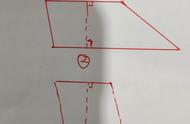
认识梯形的基础和困难是什么?学生存学习梯形之前已经认识了长方形、正方形、平行四边形的特征,知道了平行、相交与垂直,还能动手在点子图或方格纸上画长方形、正方形和平行四边形,并且会画平行线和垂线。这些为学习梯形奠定了知识、技能基础。梯形虽然是学生初次接触,但在实际牛活中,学生都接触过梯形原型,有一定的生活经验,只是很难准确地抽象出它的本质属性。另外,对于梯形的高的理解和作法上存在一定的难度。
怎样引导学生去认识梯形、发现它的特征呢?丁杭樱老师利用点子图研究图形的特征,收到了很好的效果。①回忆已经认识了哪些四边形,并在点子图出几个不一样的四边形。点子图不仅便于学生比较准确地画图,还利于学生发现不同四边形的特点,因力它能把平面图形的点、线、面联系起来,促使学生快速发现边和角的特征。②在分类比较中认识特殊的梯形。在学生画出的不同的四边形中找出梯形。如果学生作品中没有出现梯形,老师可以做一些适当补充,让学生去判断辨别,最终发现等腰梯形和直角梯形的特性。③分析量的变化(边的长短、角的大小)如何影响图形的变化。丁老师提出问题:四根长度相等的小棒能围成什么图形?(正方形或菱形)然后把四根小棒分成两组,每组两根长度相等、两组之间长度不等,问:这样的四根小棒能围成什么图形?(平行四边形、长方形)丁老师接着问:把其中一根换成短一点的,又可以围成什么图形呢?(等腰梯形、直角梯形)小棒的出现使图形的认识不再局限于单一的形,量的变化能引起形的变化,小棒把数与形紧密联系起来,利于学生多角度把握知识。④总结梳理串成线,形成网。丁老师进行总结性提问:任意四边形改变什么条件就能变成梯形?改变梯形的什么条件就能成为平行四边形?平行四边形又如何转变成长方形、正方形?在此基础上,丁老师引导学生梳理出关系网(如下图)。

四.推荐阅读
(1)《数学辞海·第一卷》(裘光明,山西教育出版桂,2002)
该书的第136-137页详细论述了梯形的意义和性质。
(2)《知识求多更要求联》(丁杭樱,《小学教学(数学版)》,2010年第1期)
该文巧妙运用点子图、小棒等学具帮助学生认识平行四边形和梯形等四边形的特征以及它们之间的关系,收到了好的教学效果,值得广大一线教师借鉴。
,