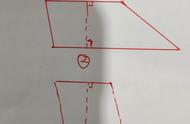
凸四边形ABCD的中线EF(连接上下对边的中点连线)把它的面积分成相等的部分。
证明这个四边形是梯形。

分析:这个题的原命题显然大家很容易证明,即梯形的平行两个边的中线把该梯形的面积平分。现在我们证明其逆定理。
证明1:我们引进一个符号,设[X]表示图X的面积。

因为AE=BE,(ΔAEF]=[ΔBEF]。由于已知[ACFE]=[BDFE],取其差,我们看到[ΔACF]=[ΔBDF]
但这两个三角形底相同CF=DF,这意味着它们到底的高度也相等,即A和B到CD的距离相等,即AM=BN, 又因为AM∥AN,所以AMNB是矩形,因此AB∥CD。
故四边形为梯形。