“三角形的内角和、多边形的内角和”,都是人教版数学四年级下册第5单元的学习内容。别看二者都是关于“内角和”的,可它们的推理方法却有异同,三角形内角和推导用的是不完全归纳法;而多边形内角和的推导,既用了不完全归纳法,还用了三段论和类比推理。下面进行具体分析:

“三角形的内角和”是三角形的一个重要性质,它有助于学生理解三角形的内角之间的关系,也是进一步学习的基础。教材第65页例6,先让学生通过“量、算”不同类型的三角形的内角度数,使学生初步感受到它们的内角和大约是180度,由于量角的时候可能会产生误差,所以这里用了“大约”二字。
然后,再通过“剪、拼、看”的活动,引导学生把三角形的三个内角剪下来拼成一个平角的方法验证三角形的内角和是180度。还可以让学生用“折一折”的方法,把三个内角拼成一个平角。在一系列的实验、操作活动中,逐步归纳出三角形的内角和。

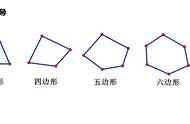
“多边形内角和”的推导是从四边形内角和开始的。教材第66页例7,先用探索三角形内角和的经验探索四边形的内角和。把四边形分为已学过的长方形、正方形、梯形等图形,通过计算长方形、正方形的内角和,得出特殊的四边形的内角和是360度。再从特殊到一般,通过“剪、拼”的实验活动得出四边形的内角和,即“把一个四边形的4个角拼在一起,从拼成的是周角得出4个角的度数和是360度”。到这里,上述这些推导方法都属于合情推理中的不完全归纳法。

如果每个多边形内角和都像上面用“剪、拼”的方法进行推导,那就太麻烦了,所以多边形的内角和还可以用“转化法”进行推导,即把四边形分成2个三角形,借助三角形的内角和是180度得出四边形的内角和是180度×2=360度。由此类推得出五边形的内角和是180度×3=540度,因为五边形可以分成3个三角形;那么六边形的内角和就是180度×4=720度;七边形的内角和是180度×5=900度……上述这些用的是演绎推理中的三段论,例如:三角形的内角和是180度为大前提,四边形可以分成2个三角形为小前提,结论就是四边形的内角和是180度×2=360度。其中还呈现了类比推理的思想。

接下来,进一步引导学生在转化中观察发现:每次转化后的三角形个数都比多边形边数少2,所以根据这个关系可以推导出这样的算式:四边形的内角和=180度×(4-2);五边形的内角和=180度×(5-2);六边形的内角和=180度×(6-2);七边形的内角和=180度×(7-2)……以此类推,n边形的内角和=180度×(n-2)。让学生在探究规律的过程中获得合情推理的经验。上述这个推导过程中既用了不完全归纳法,又呈现了三类比推理的方法。

“三角形内角和”与“多边形内角和”的知识在人教版数学初中二年级上册第1单元还有进一步的学习。教材第11页用数学证明的方法,精准的得出三角形的内角和是180度的结论,感兴趣的同学可以看看哦。
,