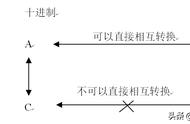
如题a的值是多少呢?答案是a=1024。什么是不是觉得有点神奇。这是学计算机的基础知识是关于数是如何在计算中如何表示的问题。下面我们来看看为什是1024呢?
数的表达
计算机中的数表示都是二进制表示,在计算机的眼里正负数是都是0和1的组成,符号本身也是数值化的。通常采取最高位表示符号,0表示为正,1表示为负数。常用的编码有原码、补码、和反码。而我们现在的计算机采用的就是补码。
补码正数的表示以最高位有效位为0,其余表示数的绝对值。如在8位的机器中 [ 1] = 00000001,那么负数如何表示呢?负数等于 2的n次方,这里的n是机器的位长, 减去它的绝对值,如[-1] = 2^8-1 = 11111111。
那么有没有更快的方法求负数的补码呢?答案是肯定的 ,只需将正数按位取反然后加1就得到正数的补码了,如1的补码是 0000 0001 按位取反后得 1111 1110 再加1 得 1111 1111 结果跟上面一致的。
通过上面我们可以发现同样的原理正数的补码也是可以通过负数求得,运算的方法跟通过正数求负数的一致,也就是说 ~x 1 = -x,这就是我们书上说的求补运算,这也是a=~1024 1 ;a=1024 的原因。
数表示成补码后计算机就可以直接按二进制的加法运算进行计算了,也不需管数是正数还是负数的问题,因为符号本身也符号化了。
,