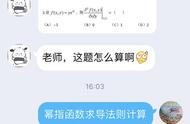
求函数y=(32x^3 11x 7)^4的导数
- 主要内容:
本文通过幂函数复合函数求导法、取对数求导法等,介绍函数y=(32x^3 11x 7)^4的一阶导数和二阶导数计算的主要步骤。
- 幂函数导数法:
此时看成是幂函数的复合函数,用链式求导,即:
∵y=(32x^3 11x 7)^4,即y=u^4,u=32x^3 11x 7,
∴y'=4*u^3*u’x=4*u^3*(96x^2 11),
即:y'=4(96x^2 11)(32x^3 11x 7)^3。

- 取对数求导法:
y=(32x^3 11x 7)^4,两边取对数得:
lny=ln(32x^3 11x 7)^4=4ln(32x^3 11x 7),
两边同时对x求导,得:
y'/y=4*(32x^3 11x 7)'/(32x^3 11x 7)
y'/y=4*(96x^2 11)/(32x^3 11x 7),进一步变形有:
y'=4(32x^3 11x 7)^4*(96x^2 11)/(32x^3 11x 7)
=4(32x^3 11x 7)^3*(96x^2 11)。
- 二阶导数计算:
使用函数乘积求法:
因为y'=4(96x^2 11)(32x^3 11x 7)^3,再次对x求导,所以:
y''=4[192x^1*(32x^3 11x 7)^3 (96x^2 11)*3*(32x^3 11x 7)^2*(96x^2 11)]
= 4[192x^1*(32x^3 11x 7)^3 (96x^2 11)^2*3*(32x^3 11x 7)^1]
= 4(32x^3 11x 7)^2*[192x^1*(32x^3 11x 7)^1 (96x^2 11)^2*3]
- 取对数求法:
对y'=4(96x^2 11)(32x^3 11x 7)^3取对数有:
ln y'=ln[4(96x^2 11)(32x^3 11x 7)^3]
=ln4 ln(96x^2 11) 3*ln(32x^3 11x 7)
两边同时对x再次求导,则:
y''/y’=192x^1/(96x^2 11) 3*(96x^2 11)/(32x^3 11x 7),进一步化简为:
y''= 4(96x^2 11)(32x^3 11x 7)^3*[192x^1/(96x^2 11) 3*(96x^2 11)/(32x^3 11x 7)]