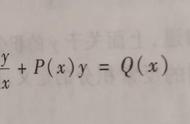微分方程是指包含未知函数及其导数,并且未知函数是一元函数的方程。这种方程在自然科学和工程技术的许多领域,如物理学、化学、生物学、工程学等,都有广泛的应用。因此,微分方程在数学中占据着非常重要的地位。
一、微分方程的分类
根据未知函数及其导数的个数,微分方程可以分为常微分方程和偏微分方程两大类。常微分方程是指未知函数及其导数是一元函数的方程,而偏微分方程是指未知函数及其导数是多元函数的方程。
二、微分方程的解
微分方程的解是指满足微分方程的函数,这个函数可以使得微分方程的等号成立。求解微分方程的目标就是找到这样的一个函数。通常,微分方程的解会具有某些特性,比如连续性、可微性等。
三、微分方程的求解方法
求解微分方程的方法有很多种,其中比较常用的有分离变量法、积分因子法、常数变易法等。这些方法的使用取决于微分方程的具体形式和性质。在求解微分方程的过程中,我们还常常需要利用一些数学工具,比如积分表、微分表等。
四、微分方程的应用
微分方程在许多领域都有广泛的应用。比如在物理学中,微分方程可以用来描述物体的运动规律;在化学中,微分方程可以用来描述化学反应的动力学过程;在生物学中,微分方程可以用来描述人口动态等。
总之,微分方程是一门非常重要的数学科目,它不仅在数学领域有着重要的地位,而且在其他许多领域也有着广泛的应用。通过学习微分方程,我们可以更好地理解和掌握各种复杂的现象和规律。