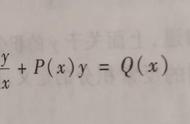常微分方程是由数学家Newton和Leibniz在17世纪同时独立发明的。其中,Newton主要研究力学问题,Leibniz则研究光学和物理学问题。他们分别使用不同的符号和方法来表达和求解常微分方程,但都为这一领域的发展做出了重要贡献。
在随后的几个世纪里,欧拉、拉格朗日、拉普拉斯、高斯等数学家进一步完善和推广了常微分方程的理论和方法,使其成为现代数学的重要分支之一。常微分方程不仅在数学本身中发挥着重要作用,而且在自然科学、工程技术和社会科学等领域中也具有广泛的应用。
常微分方程是指只涉及一元函数的导数及其各阶导数的方程。通常表示为 :

是未知函数,f 是已知函数,n 为方程的阶数。
常微分方程是数学的一个重要分支,广泛应用于自然科学、工程技术和社会科学等领域,例如物理、化学、生物学、经济学和金融学等。常微分方程的解法可以分为解析解和数值解两种方法。解析解是指可以用一定的代数和函数分析技巧求得的精确解,数值解则是通过数值计算方法来求解的近似解。
常微分方程是数学中的一个重要分支,具有广泛的应用和重要性,主要有以下几个方面的用途:
- 自然科学:常微分方程在物理学、化学、生物学等自然科学领域中有着广泛的应用。例如,描述运动物体的牛顿定律、描述放射性衰变的指数衰减定律、描述生物种群变化的Logistic方程等都是常微分方程。
- 工程技术:常微分方程在工程技术领域中也有着广泛的应用。例如,描述电路中电压和电流的关系、描述电动机的运动过程、描述化工过程中的物质转移等都是常微分方程。
- 社会科学:常微分方程在经济学、金融学等社会科学领域中也有着应用。例如,描述经济增长的Solow模型、描述股票价格波动的Black-Scholes方程等都是常微分方程。
- 数学本身:常微分方程作为数学的一个分支,不仅具有广泛的应用,而且也是数学的重要研究对象。研究常微分方程的解法、特殊解、稳定性等性质,不仅有助于深化数学理论,而且也有重要的应用价值。
因此,常微分方程作为数学中的一个重要分支,在自然科学、工程技术和社会科学等领域中都具有广泛的应用和重要性。
三、常微分方程有哪些有意思的应用常微分方程在自然科学、工程技术、社会科学等领域中有着广泛的应用,以下是其中一些有趣的应用:
- 调和振动:调和振动是一种重要的物理现象,它可以用常微分方程来描述。例如,弹簧振子、摆钟等都可以用二阶线性常微分方程来描述。
- 阻尼振动:阻尼振动是指振动物体受到阻力影响而逐渐减弱的振动。常微分方程可以描述阻尼振动的过程,例如,可以用二阶线性常微分方程来描述受到粘性阻力影响的弹簧振子的运动过程。
- 生物种群动力学:生物种群动力学是指研究生物种群数量随时间变化的规律和机制的学科。其中,许多问题可以用常微分方程来描述,例如,生物种群的增长、衰退、竞争等。
- 金融学中的Black-Scholes方程:Black-Scholes方程是一种用于定价金融衍生品的偏微分方程,它的背后原理是通过对股票价格的变化建立数学模型,预测期权的价格。
- 水平飞行器:水平飞行器是一种特殊的飞行器,它的翼面可以自动调整以保持水平飞行状态。常微分方程可以用于描述水平飞行器的运动状态,帮助设计飞行控制系统。
这些有趣的应用显示了常微分方程在不同领域中的应用价值和重要性。
,