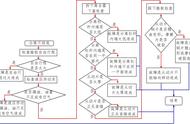
只要AB=BA,且A和B都可对角相似化,那么A和B的特征向量就相同。
1)如果都是对称矩阵,那么特征值相同,能推出合同
2)如果两矩阵都可以相似对角化,则两矩阵特征值相同,能推出相似。
扩展资料:
在数学中,矩阵(Matrix)是一个按照长方阵列排列的复数或实数集合 ,最早来自于方程组的系数及常数所构成的方阵。这一概念由19世纪英国数学家凯利首先提出。
矩阵运算在科学计算中非常重要 ,而矩阵的基本运算包括矩阵的加法,减法,数乘,转置,共轭和共轭转置 。
不能够相似对角化, 那么可以举出反例(Jordan型),
有两个特征值 和 , 各自的特征向量是 和 , 但不是对称矩阵.
2. 能够相似对角化(即为正规矩阵, 满足 ),
2.1 如果可以有复特征值的话, 那么可以举出反例(Schur型),
2.2 可以相似对角化, 又只有实特征值, 那么必然可以正交对角化, 即存在正交矩阵 , 使得 , 为对角矩阵, 则 必然为对称矩阵, 证明是显然的.