计算机0和1的工作原理,计算机中0和1代表什么

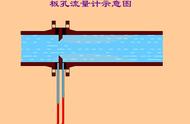
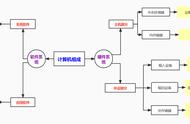
图0-36 计算机硬件设备的三角形图解

提到计算机，就不得不提及在计算机的发展史上做出杰出贡献的著名应用数学家冯·诺依曼（Von Neumann），是他带领专家提出了一个全新的存储程序的通用电子计算机方案。这个方案规定了新机器由5个部分组成：运算器、逻辑控制装置、存储器、输入和输出（如图0-37所示）。并描述了这5个部分的职能和相互关系。这个方案与早期的ENIAC相比，有两个重大改进：一是采用二进制；二是提出了“存储程序”的设计思想，即用记忆数据的同一装置存储执行运算的命令，使程序的执行可自动地从一条指令进入到下一条指令。这个概念被誉为计算机史上的一个里程碑。计算机的存储程序和程序控制原理被称为冯·诺依曼原理，按照上述原理设计制造的计算机称为冯·诺依曼机。

图0-37 计算机的组成框架

简单概况，冯·诺依曼计算机结构包含3条重要的设计思想，具体如下。

• 计算机应由运算器、控制器、存储器、输入设备和输出设备5大部分组成。
• 以二进制的形式表示数据和指令。
• 程序预先存入存储器中，计算机在工作中能够自动地从存储器中取出程序指令并加以执行。

指令是能被计算机识别并执行的二进制代码，它规定了计算机能够完成的某一种操作。一条指令通常由如下两个部分组成：

• 操作码：它用于指明该指令要完成的操作，如存数、取数等。操作码的位数决定了一个机器指令的条数。当使用定长度操作码格式时，若操作码位数为n，则指令条数可有2n条。
• 操作数：它是指操作对象的内容或者所在的单元格地址。在大多数情况下是地址码，地址码有0~3位。从地址代码得到的仅是数据所在的地址，既可以是源操作数的存放地址，也可以是操作结果的存放地址。

计算机的工作过程实际上是快速地执行指令的过程。计算机在工作时，共有两种信息在流动，一种是数据流，另一种是控制流。

数据流是指原始数据、中间结果、结果数据、源程序等。控制流是由控制器对指令进行分析、解释后向各部件发出的控制命令，用于指挥各部件协调地工作。

下面，通过指令的执行过程来认识计算机的基本工作原理吧！计算机的指令执行过程可分为如下几个步骤。

1）取指令。从内存储器中取出指令送到指令寄存器。

2）分析指令。对指令寄存器中存放的指令进行分析，由译码器对操作码进行译码，将指令的操作码转换成相应的控制电信号，并由地址码确定操作数的地址。

3）执行指令。它是由操作控制线路发出的完成该操作所需要的一系列控制信息，以完成该指令所需要的操作。

4）为执行下一条指令作准备。形成下一条指令的地址，指令计数器指向存放下一条指令的地址，最后控制单元将执行结果写入内存。

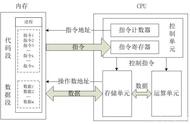
上述步骤走完，也就完成了一条指令，一条指令的执行过程叫做一个“机器周期”。指令的执行过程如图0-38所示。

图0-38 指令的执行过程

计算机在运行时，CPU从内存读取一条指令到CPU内执行，指令执行完毕，再从内存读取下一条指令到CPU执行。CPU不断地读取指令、分析指令、执行指令，再读取下一条指令，这就是程序的执行过程。

总之，计算机的工作就是执行程序，即自动连续地执行一系列指令，而程序开发人员的工作就是编制程序，使计算机持续地工作。

由于计算机是通过电位记录信息的，因此仅能识别0和1这两个数字，故而在计算机内部，数据都是以二进制的形式存储和运算的，下面就来介绍计算机数据的常用计量单位。

计算机存储数据的最小单位为 位(bit)，中文称为比特，一个二进制位只能表示0或1两种状态，要表示更多的信息，则要把多个位组合成一个整体，一般以8位二进制组成一个基本单位。由于比特这个单位太小了，因此用比特作为单位的情况比较少，网络带宽速率一般用Mbit/s来表示，正常的下载速度就是1Mbit/s=128KBytes/s，这就是我们购买了1MB的带宽，而实际下载速度为128KBytes/s的原因。

字节是计算机数据处理的基本单位。 字节（Byte）简记为B，规定1字节为8位，即1B=8bit。每个字节由8个二进制位组成。一般情况下，一个ASCII码占用1字节，一个汉字占用2~4个字节。

1Byte=8bit，1KB=1024B，1MB=1024KB，1GB=1024MB，1TB=1024GB，1PB=1024TB，1EB=1024PB，1ZB=1024EB，1YB=1024ZB，1DB=1024YB，1NB=1024DB。

用若干数位（由数码表示）的组合去表示一个数，各个数位之间是什么关系，即逢“几”进位，这就是进位计数制的问题。也就是数制问题。数制，即进位计数制，是人们利用数字符号按进位原则进行数据大小计算的方法。通常是以十进制来进行计算的。另外，还有二进制、八进制和十六进制等。

在计算机的数制中，要掌握3个概念，即数码、基数和位权。下面简单地介绍这3个概念。

• 数码：一个数制中表示基本数值大小的不同数字符号。例如，八进制有8个数码，即0、1、2、3、4、5、6、7。
• 基数：一个数值所使用数码的个数。例如，八进制的基数为8，二进制的基数为2.
• 位权：一个数值中某一位上的1所表示数值的大小。例如，八进制的123，1的位权是64，2的位权是8，3的位权是1。

十进制的特点具体如下。

• 包含10个数码：0、1、2、3、4、5、6、7、8、9。
• 基数：10。
• 逢十进一（加法运算），借一当十（减法运算）。
• 十进制转换十进制计算式说明：
• 例如，将一个整数123456转换为十进制表示的计算式为：
• 123456=110^5 210^4 310^3 410^2 510^1 610^0

二进制的特点具体如下。

• 包含两个数码：0、1。
• 基数：2。
• 逢二进一（加法运算），借一当二（减法运算）。
• 二进制转换为十进制的计算式举例说明如下。
• 例如，将一个二进制数1101转换为十进制表示的计算式为：
• 12^0 02^1 12^2 12^3=13

八进制的特点具体如下。

• 包含8个数码：0、1、2、3、4、5、6、7。
• 基数：8。
• 逢八进一（加法运算），借一当八（减法运算）。
• 八进制转换为十进制的计算式举例说明如下。
• 例如，将一个八进制数123转换为十进制的计算式为：
• 38^0 28^1 1*8^2=83

十六进制特点具体如下。

• 包含16个数码：0、1、2、3、4、5、6、7、8、9、A、B、C、D、E、F。
• 基数：16
• 逢十六进一（加法运算），借一当十六（减法运算）。
• 在16个数码中，A、B、C、D、E和F这6个数码分别代表十进制的10、11、12、13、14和15，这是国际上通用的表示法。
• 十六进制转换为十进制的计算式举例说明如下。
• 例如，将一个十六进制数5F3A转换为十进制的计算式为：
• 1016^0 316^1 1616^2 516^3=24634
• 二进制数与其他数之间的对应关系如表0-6所示。
• 表0-6 几种常用进制之间的对照关系