“24点”游戏秘籍
“24点”数学游戏,它能把枯燥的基本数字计算变得趣味盎然,能大大提高计算能力和计算速度,使得思维灵活敏捷,是一种寓教于乐的的智力竞赛游戏。
游戏规则:给定4个自然数,通过加、减、乘、除四则运算,可以任意交换数的位置,可以随意的添加括号,但是每个数只能且必须用上一次,连起来组成一个计算式子,得数就是24。
“24点”数学游戏通常是用扑克牌进行的,此时,给定的4个数就被限定在1~13的范围内。“24点”数学游戏可以是1个人玩,也可以是多人玩,比如4个人玩,把扑克牌中的大、小王拿掉,剩下的52张牌洗好后,每人分给13张,然后就是每人出一张牌,其中J、Q、K分别代表11、12、13,其他的牌就代表相应的1~10的自然数,谁先算出“24点”,谁就把这4张牌赢走,然后继续玩牌,最后谁的牌多谁就获胜。当如果算不出“24点”的话,各自就拿回来自己的牌,然后洗牌,再次继续进行。
要想算得又快又准,这就要靠平时的基本功了,而要有好的过硬的基本功,就要多练习了,只有多练,才能算得好,而且这又能很好地锻炼自己的反应能力和敏捷的判断能力,对学好数学很有帮助。而要玩好这个游戏,最重要的有2条:
1、熟悉加法口诀和乘法口诀;
2、利用括号,因为括号既能改变运算顺序,也可以改变运算符号。
下面通过一些例子来说明“24点”的一些基本算法。
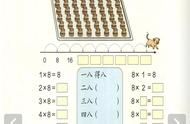
“24点”的基本算法(1)乘法乘法式子有3×8=24,4×6=24,2×12=24,1×24=24等。
例1.3、3、5、6解法一、根据3×8=24,3已经有了,只要将其他3个数凑成8,有3×(5 6-3)=24。
解法二、根据4×6=24,6已经有了,只要将其他3个数凑成4,有6×(5-3÷3)=24或者6×(3×3-5)=24。
解法三、还是根据3×8=24,要将2个数凑成3,要将另2个数凑成8有(6-3)×(5 3)=24。
解法四、先把其中两个数相乘,积不足24的用另外2个数补足,有3×5+3+6=24
解法五、先把其中两个数相乘,积超过24的用另外2个数割去,有5×6-3-3=24
例2.2、2、4、8解法一、根据3×8=24,8已经有了,只要将其他3个数凑成8,有8×【(2 4)÷2】=24或者8×【4-2÷2】=24。
解法二、根据4×6=24,4已经有了,只要将其他3个数凑成6,有4×(2+8÷2)=24。
解法三、根据2×12=24,有2×(2×8-4)=24。
解法四、根据8+16=24,8已有,将其他3个数凑成16,有8+2×2×4=24或者8+(2+2)×4=24。
解法五、根据4+20=24,4已有,将其他3个数凑成20,有4+(2+8)×2=24。
“24点”的基本算法(2)除法除法式子有24÷1=24,48÷2=24,72÷3=24,96÷4=24等。
例1.2、4、8、10解法一、根据48÷2=24,2已经有了,只要将其他3个数凑成48,有(4×10+8)÷2=24。
解法二、不过容易想到2×12=24,故有(2+10)×(8÷4)=24。
解法三、根据96÷4=24,有【(2+10)×8】÷4=24。
解法四、根据4×6=24,4已经有了,只要将其他3个数凑成6,有4×(2×8-10)=24。
解法五、由乘减有:4×10-2×8=24。
例2.2、3、7、10解法一、根据72÷3=24,3已经有了,只要将其他3个数凑成72,有(7×10+2)÷3=24。
解法二、由乘减知道:2×10+7-3=24。
例3.4、6、9、10解法一、根据24÷1=24,有(4×6)÷(10-9)=24。
解法二、根据96÷4=24,4已经有了,只要将其他3个数凑成96,有(9×10+6)÷4=24。
“24点”的基本算法(3)借助“乘法分配律” 例、1、4、4、5分析:很明显,4×(1+5)=24。但是这3个数就凑成了24了,可惜还有一个数4用不到,根据规则,必须要将这个4用进去,怎么办?用到“乘法分配律”试试。
解:4×1+4×5=24。
例2、6、8、8、98×(9-6)=8×9-8×6=24
例3、5、7、12、12
12×(7-5)=12×7-12×5=24
总结:在例1~例3中,我们用到了a×(b+c)=a×b+a×c, a×(b-c)=a×b-a×c 例4、2、2、6、9分析,显然,有2×9+6=24,三个数就够了,但是还有一个数字2没有用到,这次又怎么办呢?
还是利用“乘法分配律”,24=2×9+6=2×9+6÷2×2=2×(9+6÷2)=24
“24点”的基本算法(4)分数 例1、1、5、5、5分析:假设基本算式已经找到:5×?=24,则?= .用1,5,5能够凑成 吗?
解: =5- ,于是得到5×(5-1÷ )=24。
例2、3,3,8,8
分析:我们有基本算式8÷ =24。被除数8已有,另外三个数3,3,8能够凑成 吗?
解: =3- ,于是有8÷(3-8÷3)=24。
例3、1,4,5,6解:根据4÷ =24,有4÷(1-5÷6)=24。 或者6÷ =24,有6÷(5÷4-1)=24。
例4、2、6、9、9
2×9+6=2×9+6÷9×9=9×(2+6÷9)=24
例5、2、4、10、10
2×10+4=2×10+4÷10×10=10×(2+4÷10)=24
总结:在例1~例5中,我们用到了a×b+c=a×(b+c÷a), a×b-c=a×(b-c÷a).我们知道,符合“24点”数学游戏规则的每个具体的算式中,一定要知道出现四个数和三个运算符号。也就是说,一定要进行三次运算,出现三个运算结果。其中前两次结果是运算过程中的中间结果,第3次即最后一次的运算必须是24。
以上是从运算定律这方面总结的,下面就数与数之间的关系的计算技巧加以总结。
“24点”的基本算法(5)相连数的计算方法1、 两个数相连:四张牌中经常会出现这种情况,概率最高。能熟练的掌握运用俩个数相连的计算规律,可大大加快演算速度。
⑴两个相连数可看作1
例如:3、6、8、9 (9-8 3)×6=24 2、8、7、8 (8-7 2)×8=24
⑵两个相连数可以不参与计算,如:3、8、2、3和4、6、8、7。
⑶两个相连数也可以相乘,但是数较大时不宜采用
5、6、1、5 5×6-1-5=24或8、9、1、2 8×9÷(1+2)=24。
当四张牌中如何一组两个数相连而且另外两张牌有下列情况时都可解。即是7、3,9、3,8、2,
8、3,8、4,3、6,4、6,5、6,5、4,7、4。
2、 三个数相连⑴可以看成三个相连数中最前面一个数。如:4、5、6、6和3、4、5、8。
⑵可以看成三个相连数中中间一个数。如:3、7、8、9和2、3、4、8。
⑶可以看成三个相连数中最后面一个数。如:2、3、4、6和6、7、8、3。
⑷可以看成三个相连数中最前面一个数减去1。如:4、5、6、8和5、6、7、6。
⑸可以看成三个相连数中最后面一个数加上1。如:3、4、5、4和5、6、7、3。
⑹可以看成三个相连数中中间一个数的2倍数。如:2、3、4、4和7、8、9、8。
⑺可以看成三个相连数中中间一个数的3倍数。如:6、7、8、3和8、9、10、3。
⑻三个数相连时,有时可以看作是两组两个数相连,如3、4、5可看作3与4或4与5两组两个数相连,计算时具体用哪个组合要看另一张牌的数。
3、 四个数相连:四个数相连的概率极小,一共只有7个组合,每个组合都有解,不难。 “24点”的基本算法(6)相同数的计算方法 1、 两个数相同⑴两个数相同可以看作1。如5、5、2、8和7、7、3、6。
⑵两个数相同可以看作0。如7、7、3、8和9、9、4、6。
⑶两个数相同可以看作这个数的2倍。如5、5、2、7和4、4、2、6。
⑷两个数相同可以看作乘积,数较大时不宜使用。如5、5、2、1和3、3、6、8。
从上面的例子知道,当四张牌中出现任何一对数相同时,另两张牌如果是3和8,或者是4和6时则可解。并且根据两个相同数可以看作1的道理,四张牌中有两个相同,另外两张是下列情况时均可解。如9、9、7、3。(9÷9+7)×3=24,9、9、5、4。(5+9÷9)×4=24
9、9、9、3。(9-9÷9)×3=24,9、9、2、8。(2+9÷9)×8=24
9、9、8、3。(9÷9)×3×8=24,9、9、4、8。(4-9÷9)×8=24
9、9、6、3。(3+9÷9)×6=24,9、9、5、6。(5-9÷9)×6=24
9、9、7、4。(7-9÷9)×4=24,9、9、6、4。(9÷9)×6×4=24。
2、 三个数相同⑴三个数相同时可以看作是其中的一个数,如3、3、3、8和4、4、4、6。
⑵三个数相同时可以看作是其中的一个数加上1,如5、5、5、4和7、7、7、3或7774。
⑶三个数相同时可以看作是其中的一个数减去1,如5、5、5、6和9、9、9、3。
从上面的例子可以知道,四张牌中出现三个相同数时,可以看作3个不同的数。如出现7、7、7时,可看作是6,7,8,当另外一个数是3或4时,应用此法便可解答。如出现3个4时,可看作3、4、5,当另一个数是6或8时,也可解。其他依此类推。
3、 四个数相同:四个数相同出现的概率较少,一共有10个。这些组合中,只有四个3、4、5、6能够解答,其余的都没有解。 “24点”的基本算法(7)单数的计算方法 1、 一个单数随机取出的四张牌中几乎都会出现一张单数。当出现一张单数时,应根据这张单数的数目和另外三张双数之间的关系来做灵活调整。因为有3×8=24的基本算法,所以如单数是3,一般可以考虑把三个双数处理成8。如3、10、2、4有3×(10 2-4)=24或3、2、2、4有3×(2 2+4)=24。
如单数不是3,双数中有8时,可以将单数和其他两个双数处理成3。例如9、4、2、8有8×(9-2-4)=24或者9、10、2、8有8×(10-9+2)=24。
单数既不是3,双数不是8呢,有时可以将通过一个单数与2个双数和一个双数进行匀算后出现3和8,如9、6、4、4有(9-6)×(4+4)=24或9、6、2、4有(9-6)×2×4=24。
用以上方法不能求解时,就要考虑其他方法了。可将单数乘上双数变成一个双数后再和另外两个双数一起运算。在单数较大时可先减掉一个双数再乘上一个双数变成双数,再和另外一个双数运算。通常就是乘减或乘加运算。如3、4、6、6有3×4+6+6=24。3、4、2、6有3×4+2×6=24,9、6、4、2有(9-6)×2×4=24。
2、 二个单数:可以通过二个单数之间相加或相减变成双数。如3、3、2、2有(3+3)×(2+2)=24,9、3、8、2有(9-3)×8+2=24。
一般两个单数之间不宜相乘,因为相乘后又是单数。且数目较大,但是有例外。如7、7、1、2有(7×7-1)÷2=24。但是两个单数可以相除的话,不妨一试。如9、3、2、6有9÷3×(2+6)=24或9、3、4、4有9÷3×(4+4)=24。