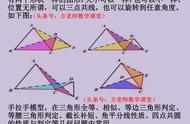
今天我们来看一个八年级上学期的几何题。
如图,AM、CM分别平分∠BAD和∠BCD,若∠B =42°,∠D=54°,求∠M的度数.

这个题是与角平分线有关的三角形内角和问题,难度一般,根据三角形内角和定理、角平分线的定义可以求出。一般同学解题时一步步来是可以求出角度的,就是废点时间,如果是填空题或选择题我们有没有快速解题的办法了?今天我们来用学霸思维看看怎么5秒口算出答案。
我们来回顾下最近总结过的“蝴蝶模型”:

蝴蝶模型结论:∠A ∠B = ∠C ∠D ,证明方法:三角形内角和定理。
观察上题的图形,我们可以拆分成2个蝴蝶模型,直接上结论有:
∠B ∠BAD=∠D ∠BCD,∠M ∠MAD=∠D ∠DCM,
AM、CM分别平分∠BAD和∠BCD,所有∠BAD=2∠MAD,∠BCD=2∠DCM,
∠B =42°,∠D=54°,变式得∠M=(42° 54°)/2=48°
这就是模型的魅力,帮你快速解题,得心应手,当然提前是要熟练掌握各种模型的基本图形,在做题的过程中学会灵活运用!
上面专栏详细讲解了八年级上学期必会的各种模型,还有经典例题、习题搭配练习,都配有超详细的答案解析,学生自学也完全适用,如果有不明白的地方,也可以私聊老师或下方评论区留言互动,老师都会第一时间解答的。
还提供免费的电子版课件以及2019年八上数学期中考试题型分类汇编资料。
【往期精彩推荐】
,