通过观察,可以发现,阴影部分的面积是整个圆面积的一半,因此飞镖落在阴影部分的概率等于1/2.
03题型三:树状图或列表法
例题5:2021秋开学为防控冠状病毒,学生进校园必须戴口罩,测体温.某校开通了三条人工测体温的通道,每周一分别由王老师、张老师、李老师三位老师给进校园的学生测体温(每个通道一位老师),每名学生在3个通道中可随机选择其中的一个通过.若甲、乙两名同学周一不同时进入校园,解决以下问题:
(1)求甲周一进校园由王老师测体温的概率;
(2)求甲、乙周一进校园分别由不同老师测体温的概率.
解:(1)甲周一进校园由王老师测体温的概率为1/3;
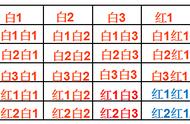
(2)把王老师、张老师、李老师三位老师分别记为A、B、C,画树状图如下:

共有9种等可能的结果,甲、乙周一进校园分别由不同老师测体温的结果有6种,
∴甲、乙周一进校园分别由不同老师测体温的概率为6/9=2/3.

例题6:阳光花园小区设置了“可回收物”、“有害垃圾”、“厨余垃圾”、和“其他垃圾”四种垃圾箱,分别记为A、B、C、D.
(1)快递包装纸盒应投入();(2)小明将“弃置药品”随机投放,则她投放正确的概率是();(3)小丽将二种垃圾“废弃食物”(属于厨余垃圾,记为C)、“打碎的陶瓷碗”(属于其他垃圾,记为D)随机投放,求她投放正确的概率.
解:(1)快递包装纸盒应投入A垃圾箱;
(2)小明将“弃置药品”随机投放,则她投放正确的概率是1/4;
(3)画树状图如下:

由树状图知,共有16种等可能结果,其中她投放正确的只有1种结果,
∴她投放正确的概率为1/16.
04类型四:已知概率求数量
例题7:在一个不透明的盒子中装有n个小球,它们除颜色不同外,其余都相同,其中有4个是白球,每次试验前,将盒子中的小球摇匀,随机摸出一个球记下颜色后再放回盒中,大量重复上述实验后发现,摸到白球的频率稳定在0.4,那么可以推算出n大约是()
解:∵通过大量重复试验后发现,摸到红球的频率稳定于0.4,∴4/n=0.4,解得:n=10.
利用大量重复实验时,事件发生的频率在某个固定位置左右摆动,并且摆动的幅度越来越小,根据这个频率稳定性定理,可以用频率的集中趋势来估计概率,这个固定的近似值就是这个事件的概率。
例题8:在不透明的袋子中装有北京冬奥会吉祥物“冰墩墩”和冬残奥会吉祥物“雪容融”的纪念卡片12张,每张卡片除吉祥物外其他完全相同,从中任意拿出一张,拿到“冰墩墩”纪念卡片的概率为P1,拿到“雪容融”纪念卡片的概率为P2,且P1-P2=0.5,那么袋子中“冰墩墩”纪念卡片的张数是()
解:根据题意得P1-P2=0.5,P1 P2=1,解得P1=0.75,则袋子中“冰墩墩”纪念卡片的张数是12×0.75=9(张)