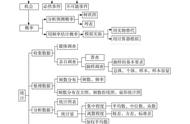
中考数学中,概率题几乎是必考题,每年中考赋予的实际情境都不同,但考查的内容都是一样的,那就是利用列表或画树状图的方法求等可能事件的概率,题目本身都很简单,但是一定要注意解题步骤及书写规范,不然很容易丢分的。
习惯上,人们画树状图比较多,因为列表需要用尺子画表格,稍麻烦些。
一、解题步骤及书写规范共分3个步骤:
1、列表或画树状图
2、根据表格或树状图描述n和m
3、把n和m代入公式P(A)=m/n求解
下面就这三个步骤中需要注意的问题分别阐述下。
1、列表或画树状图.
①转化分解
把一个事件转化分解为2~3个步骤,比如4个球中随机摸2个,本来是同时进行的一件事可以转化分解为两个步骤:先摸一个球,再摸一个球。再比如2男2女中随机抽取2个人,也可分2个步骤:先选一个,再选一个。
初中列表或画树状图求概率和高中排列组合计算概率不同,高中要“先分类,后分步”,这里却是“先分步,后分类”。
②注意“放回”还是“不放回”
“不放回”体现在列表上就是对角线为空,体现在树状图上就是下一步比上一步种类少1
③关于“开始”
很多画树状图的答案上都有个“开始”

对此问题,曾请教过一些年长的同事,说是早以前的课本上有“开始”,但是后来就取消了,已经取消了很多年,所以不需要写。当然,你要是喜欢写也可以。
2、根据表格或树状图描述n和m.
描述n时要特别强调“等可能”三个字,通常有两种写法:①共有n种等可能的结果;②共有n种结果,它们的可能性都是相等的。一般用第一种的多,因为简洁明了。
描述m时通常这样说:其中A事件包含的结果共有m种。
3、把n和m代入公式P(A)=m/n求解.
代入公式时注意两点:①简单描述下事件A;②最后结果一定要化到最简,除不尽千万不要化成小数。
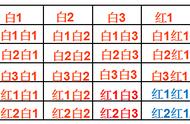
二、例题示范例、从两男两女中随机选两个人打扫卫生,求选取的两个人恰好是一男一女的概率
解:画树状图如下:

由树状图知,共有12种等可能的结果,其中选取的两人恰好是一男一女的结果有8种.
∴P(恰好一男一女)=8/12=2/3.
,