二次函数最值问题,三角形面积最值问题,中考数学里经常见到下面这种题型。给大家介绍一下常用的方法,以及学霸、学神用的秒*方法(涉及到一些高中知识,但是比较容易理解,学有余力的同学建议掌握),下面用一个例题来说明这三种不同方法,供大家参考。
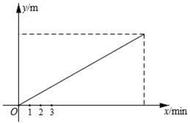
例题:如图抛物线y=-x²-x 2与y轴交于点A,与x负半轴交于点B,P是第二象限抛物线上的一个动点,求△APB面积的最大值。

中考大题需要写解题过程时,建议:铅垂法

设点P坐标(a,-a²-a 2),过点P作x轴垂线交AB于点Q(a,a 2),铅垂高PQ=-a²-a 2-(a 2)=-a²-2a,则S△PAB=PQ×|xA-xB|÷2=-a²-2a=-(a 1)² 1,所以最大值是1
下面是学霸,学神常用方法
学霸:切线法
前提知识点:
两直线平行<=>斜率相等,直线与曲线相切的概念
理解:求△APB面积的最大值,把AB当作底,相当于求高的最大值,即点P到直线AB距离的最大值。可以理解成把直线AB不断上移,当与抛物线相切时这个距离最大。如图红色直线与抛物线相切,唯一的一个交点(切点)就是所求的点P。

联立切线与抛物线:即y=x b与y=-x²-x 2
得到x b=-x²-x 2,整理后x² 2x b-2=0
※小技巧:由于交点只有一个,所以Δ=0,即2²-4(b-2)=0,解得b=3
如图过点B作BD垂直y=x 3于点D,∠CBD=45°,BC=1,BD=√2/2,即y=x 3与y=x 2的距离是√2/2,AB=2√2,所以S△PAB=1
或者利用两条平行线的距离公式:如果两直线分别为Ax By C1=0和Ax By C2=0,而且这两直线分别平行,则两条平行之间的距离公式为|C1-C2|/√ (A² B²)。
学神:导数 点到直线距离公式
前提知识点:
导数意义:曲线在某一点处的切线的斜率
y=x^n的导数:y'=nx^(n-1)
点到直线距离公式


y=-x²-x 2的导数是-2x-1,它与直线AB的斜率相等,所以-2x-1=1,x=-1,代入抛物线得到点P坐标是(-1,2)。直线AB的方程为x-y 2=0,直接代入点到直线距离公式,得到PQ=|-1-2 2|/√2=√2/2,所以S△PAB=1
利用导数可以迅速得到点P坐标,直接利用公式求出距离,所以解题速度非常快。
♡♡♡感谢大家长期的支持♡♡♡
,