中考数学函数题解题方法,中考数学必考题型及解题方法函数

转眼间，中考数学一模悄悄的落幕，距离2023年中考也就剩下最后的46天了，然而大部分学生数学成绩一直“停滞不前”。相信这一届初中毕业生都能从这次大考当中暴露出一系列的问题和漏洞。也许有些家长和学生都选择“躺平”式备考了，都在盲目性的去刷题而没有真正的去掌握和了解每个专题涉及的考点解题技巧方向。这也是为什么学生一直都说，平时感觉自己能够听的懂，也感觉自己都会了，但是在考场遇到新颖的题型变化一下就无法精准的作答了！逐一系统针对性的查漏补缺已达高效突破高分。

以下是几位资深初中毕业班学科老师特此汇编出2023年中考数学全册函数与几何全攻略：

二次函数与几何模型动点问题的背景是特殊图形,考查问题也是二次函数的有个性质和特殊图形的性质，体现的数学思想方法主要是数形结合思想和分类讨论思想。几何动点问题一直是中考热点，近几年考查探究运动中的特殊性：等腰三角形、直角三角形、、平行四边形、菱形，矩形，正方形、线段或面积的最值.

解决“动点型问题”的关键是动中求静，灵活运用“动中求静”，找到并运用不变的数、不变的量、不变的关系，建立函数关系及综合应用代数、几何知识解决问题. 根据题意灵活运用特殊三角形和四边形的相关性质、判定、定理知识确定二次函数关系式，通过二次函数解析式或函数图象判定“动点型问题”涉及的线与线关系、特殊三角形、四边形及相应的周长、面积，还有存在、最值等问题.

《专题热点精准分析》

二次函数与几何综合问题

1.二次函数与几何图形的面积问题

二次函数与几何图形的面积问题一般是利用面积公式表达出图形的面积函数关系式——一般是二次函数的表达式，再利用函数的解析式的特点求面积的最值问题；此外还会涉及到面积相等、给出面积的值等问题，其核心处理方法都是表示出面积的表达式，再去研究相关的性质.

2.二次函数与等腰三角形

在二次函数的图象中研究等腰三角形的问题，需要注意分类讨论思想的应用，找准顶角与底角是分类讨论的关键，借助等腰三角形的等边对等角、等角对等边、三线合一等性质来转化已知条件是常用的处理手段.

3.二次函数与直角三角形

在二次函数的图象中研究直角三角形的问题，需要注意分类讨论思想的应用，找准直角顶点是分类讨论的关键，借助直角三角形的勾股定理，两锐角互补等性质来转化已知条件是常用的处理手段.

4.二次函数平行四边形

在二次函数的图象中研究平行四边形的问题常会用到平行四边形的一些性质之间的转化，同时此类问题也会涉及到矩形、菱形、正方形的确定，其分析思想是互通的.

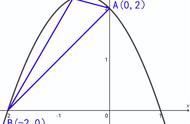
5.二次函数与线段和、差的最值问题

在二次函数的图象中研究线段的和、差最值问题，一般会用到初二所学的将军饮马问题的思想，其本质一般是三点共线问题的处理.