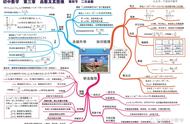
在初中的数学学习中,二次函数是非常重要的章节,而且里面涉及的考点非常的多,不管是在对应学期的各种考试,还是在中考时,都是比较热门的考点,而作为即将升入初三,面临着新的知识,同学们更应该将这部分内容理解掌握,也有利于最后的复习,今天我和同学们一起学习中考比较重要的一个基础考点,二次函数的图像与性质,这里不需要同学们死记硬背,而是学会运用观察法,比较法熟练的掌握,结合图像研究其性质及不同图像之间的相互关系,从简单的y=ax²(a≠0)开始通过分类详解,归纳总结,循序渐进的学习y=ax² bx c(a≠0),归纳出规律,从而彻底学会掌握。

一、二次函数y=ax²(a≠0)的图像和性质
二次函数y=ax²(a≠0)图象的作法:①列表:在二次函数y=ax²(a≠0)中,自变量x的取值范围是全体实数,给出x的一些代表值,求出对应的y值,一般取5个或7个点,作为顶点的原点(0,0)是必取的,然后在y轴的两侧各取2个或3个点,注意对称取点;②描点:一般先描出对称轴一侧的几个点,再根据对称性找出另一侧的几个点;③连线:按照自变量由小到大的顺序,用平滑的曲线连接所描的点,两端无限延伸。注意:二次函数y=ax²(a≠0)的图象是一条抛物线,它的对称轴是y轴,顶点是原点(0,0)。

需要特别提醒的是,二次函数以对称轴为“界”,在对称轴的左右两侧,它的增减性是恰好相反的,而且在做题的时候,一定要注意说明其图像是在对称轴的左侧还是右侧,否则可能会出现错误。在做题的时候利用图像去分析是解决问题的最有效途径,数形结合思想也是本章重要的数学思想之一。
二、二次函数y=ax² k(a≠0)的图像和性质
二次函数y=ax² k(a≠0)的图像也是一条抛物线,它是由y=ax²向上或者向下平移|k|个单位得到的。

关于y=ax² k(a≠0)的增减性其实和k的值是没有关系的,这里需要格外注意的是顶点坐标。
三、二次函数y=a(x h)²(a≠0)的图像和性质
二次函数y=a(x h)²(a≠0),它是由y=ax²向左或者向右平移|h|个单位得到的。

在学习二次函数y=a(x h)²(a≠0)的图像与性质时,可类比二次函数y=ax²的图像与性质来学习。在a相等的情况下,两个函数图像的形状、开口方向等完全相同,只是位置发生了变化。顶点坐标由(0,0)变成了(-h,0),求抛物线y=a(x h)²(a≠0)的对称轴时,只需x h=0,即可得出x=-h。
四、二次函数y=a(x-h)² k(a≠0)的图像和性质

由于从y=a(x-h)² k(a≠0)中可以直接看出抛物线的顶点坐标,因此通常也把y=a(x-h)² k(a≠0)叫做二次函数的顶点式。
五、二次函数y=ax² bx c(a≠0)的图像和性质
二次函数y=ax² bx c(a≠0)的图象的画法:(1)描点法,步骤如下:①把y=ax² bx c(a≠0)化成y=a(x-h)² k的形式;②确定抛物线的开口方向、对称轴和顶点坐标;③在对称轴两侧,以顶点为中心,左右对称描点画图。(2)平移法,步骤如下:①把y=ax² bx c(a≠0)化成y=a(x-h)² k的形式,确定其顶点(h,k);②作出函数y=ax²的图像;③将函数y=ax²的图像平移,使其顶点平移到(h,k)。

通过各种形式的二次函数图像,分类详解了他们的性质,希望同学们能够掌握,在以后的做题中,熟练运用。
,