初中数学尤其是对于刚进入初中的同学们来说,前面我们已经介绍了,初中数学主要是学会用字母来表示数,进行相关的运算和解答。而在整式的相关概念中,也已经明确了单项式、多项式、整式的相关概念,并且介绍了考点。今天我们一起来学习整式的加减,整式的加减这一节,在各地市的中考中必有涉及,尤其是同类项的概念以及去括号的法则的应用,是主要考察的内容,因此要掌握合并同类项,并且牢记这里容易出错的地方,在平时做题的反复提醒自己,养成好的习惯。我们也将通过实例来详细讲解整式的加减。

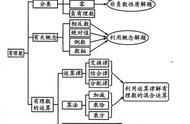
一、同类项
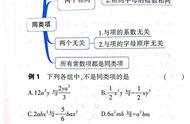
所含字母相同,并且相同字母的指数也相同的项。注意几个常数项也是同类项。“两相同”指的是:一是所含字母相同;二是相同字母的指数也相同,“两相同”同时也是判断同类项的标准,缺一不可。“两无关”:一是与系数大小无关;二是与所含字母的顺序无关。因此判断两个单项式是否为同类项只需满足两个条件即可:一是单项式所含字母相同;二是相同字母的指数也分别相同,二者缺一不可。
例题1:下列各式中哪些是同类项,为什么?
(1)、a²b与ab²;(2)、xy²与3y²x;(3)、5ab与6a²b
分析:同类项只有字母及指数有关,与系数是没有关系的,牢牢抓住上述判断依据。(1)中不是同类项,因为相同字母的指数不同;(2)、是同类项;(3)、不是同类项,因为相同字母的指数不同。
例题2:

分析:由题意可知,两个单项式相加后仍然是单项式,说明这两个单项式是同类项,根据同类项法则,可知m-1=2,n=2,得m=3,n=2.所以选c.
二、合并同类项

合并同类项的法则:同类项的系数相加,所得结果作为系数,字母和字母的指数不变,合并同类项后,所得项的系数是合并前各同类项的系数的和,且字母连同它的指数不变。合并同类项的步骤:①准确地找出同类项;②利用法则 ,把同类项的系数相加减,字母和字母的指数不变;③写出合并后的结果。合并同类项时应注意:①如果两个同类项的系数互为相反数,合并同类项后,结果为0;②最后不要漏掉不能合并的项;③只要不再有同类项,就是结果(可能是单项式,也可能是多项式)。如果题目中的多项式较多时,可以在同类项下面做相同的记号,做记号时要注意最好要连同该项的符号一同标记上,以防在合并时出错。
例题3:合并同类项: 4a² 3b² 2ab-4a²-3b²
分析:先找到式子中的同类项,然后进行系数的相加减,得到=2ab.
三、去括号法则

去括号法则:如果括号外的因数是正数,去括号后原括号内各项的符号与原来的符号相同;如果括号外的因数是负数,去括号后原括号内各项的符号与原来的符号相反。这里在做题是非常容易出错,一定要记牢,如果括号外的因数的符号是“-”时,去掉括号后,原括号内的各项都要变号,不能只改变原括号内的第一项或前几项的符号。当括号外是一个非“±1”的因数时,应根据分配律,先将该数与括号内的各项分别相乘后再去括号,以免出现错误。重点说明一下:去多重括号时,一般先去小括号,再去中括号,最后去大括号,即从内向外去括号。也可以先去大括号或中括号。如何选择去括号的顺序需要根据具体情况而定。
例题4:3(2ab﹣b)﹣2(ab﹣b)
分析:去括号时,注意易错点,就是如果括号前是“-”,一定要注意每一项都变号,还要注意的是,前面如果有因数,每一项都要乘。原式=6ab-3b-2ab 2b=4ab-b.
去括号大家明确了,相对应的就是添括号,在很多情况下为了化简计算,也可能出现添括号的情况。添括号法则:通过类比去括号法则,可以得到添括号法则,所添括号前是“ ”号,括到括号里的各项都不改变符号;所添括号前面是“-”号,括到括号里的各项都改变符号,简记为“加不变,减全变”。
,