在初中阶段,方程是解决实际问题时常用的方法。初中所学的方程包括两大类,整式方程和分式方程。
整式方程包括一元一次方程、二元一次方程组、三元一次方程组、一元二次方程。而多元方程、高次方程及分式方程,解题的基本思路最后都是化为一元一次方程。因此,让学生熟练掌握一元一次方程的解法非常重要。
对于刚升入初中的七年级学生来说,解一元一次方程的步骤较多,学生解题时非常容易出错。下面,我根据解题步骤,详解一下学生解题时易出现的错误,以及解决方法。
解一元一次方程的一般步骤有五步,第一步去分母,第二步去括号,第三步移项,第四步合并同类项,第五步未知数的系数化为1。

去分母时易出现的错误是:
一、漏乘不含分母的项。
二、没把分子部分看成一个整体,用括号括起来。
解决方法:去分母的依据是等式的基本性质2,方程的左右两边同乘以同一个数,结果仍相等。因此,去分母时,方程的左右两边应同乘以方程中各分母的最小公倍数,且约去分母后,把分子部分看成一个整体,用括号括起来。
例:

去括号时易出现的错误:
一、漏乘,没把括号外的数字与括号内各项分别相乘。
二、去括号时括号内各项的符号是否需要改变
解决方法:去括号时依据乘法分配律,括号外的数字应与括号内各项一一相乘。另外,依据去括号的法则,当括号外为正因数时,去掉括号,括号内各项的符号不变;当括号外为负因数时,去掉括号,括号内各项的符号应改变。
例: 解 2(3x-7)-5(2ⅹ 1)=4
6ⅹ-14-10ⅹ-5=4
移项时易出现错误:
一、没有理解移项的定义
二、没有改变所移项的符号

解决方法:
移项的依据是等式的基本性质1,具体做法是把方程中的某项改变符号后,从等号的一边移到等号的另一边。它和交换两项的位置是不同的。
例: 解3x-2=7x 6
3ⅹ-7x=6 2
一般把含未知数的项移到等号的左边,不含未和数的项移到右边,且先写不移动的项,后写移动的项。
合并同类项时易出现的错误:
没有弄清系数是同号还是异号,系数的绝对值是该加还是减。
解决方法:

合并同类项是依据合并同类项法则,把未知数项的系数相加。相加时应根据有理数加法法则,系数是同号,应把绝对值相加,异号时应用较大的绝对值减去较小的绝对值,应特别注意系数的符号。
例: 解、3x-7ⅹ=6 2
( 3一7 )ⅹ=8
-4ⅹ=8
系数化1时易出现错误:
一、符号
二、不能整除时,谁应是分母,谁是分子。
解决方法:
应用两数相除,同号得正,异号得负,确定商的符号。被除数是分子,除数是分母。当系数是分数时,应变为乘以它的倒数。
例:(1)、 12ⅹ=一3
x=一1/4
(2)、 一¾x=2
x=一2×4/3
ⅹ=一8/3
另外,还有一特殊步骤,当分母为小数时,常利用分数的基本性质,把小数分母化为整数分母。
例:
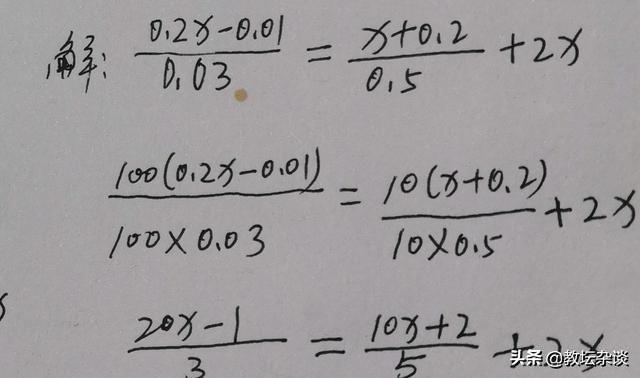
欢迎关注,希望我的解答能给你帮助。
,