人说几何很困难,难点就在辅助线。辅助线,如何添?
把握定理和概念。还要刻苦加钻研,找出规律凭经验。
等腰三角形
1. 作底边上的高,构成两个全等的直角三角形,这是用得最多的一种方法;
2. 作一腰上的高;
3 .过底边的一个端点作底边的垂线,与另一腰的延长线相交,构成直角三角形。

梯形
1. 垂直于平行边
2. 垂直于下底,延长上底作一腰的平行线
3. 平行于两条斜边
4. 作两条垂直于下底的垂线
5. 延长两条斜边做成一个三角形
菱形
1. 连接两对角 2. 做高
平行四边形
1. 垂直于平行边
2. 作对角线——把一个平行四边形分成两个三角形
3. 做高——形内形外都要注意
矩形
1. 对角线 2. 作垂线
很简单。无论什么题目,第一位应该考虑到题目要求,比如AB=AC BD....这类的就是想办法作出另一条AB等长的线段,再证全等说明AC BD=另一条AB,就好了。还有一些关于平方的考虑勾股,A字形等等
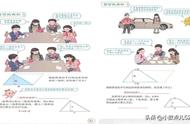
三角形
图中有角平分线,可向两边作垂线。
也可将图对折看,对称以后关系现。
角平分线平行线,等腰三角形来添。
角平分线加垂线,三线合一试试看。
线段垂直平分线,常向两端把线连。

要证线段倍与半,延长缩短可试验。
三角形中两中点,连接则成中位线。
三角形中有中线,延长中线等中线。
解几何题时如何画辅助线?
①见中点引中位线,见中线延长一倍
在几何题中,如果给出中点或中线,可以考虑过中点作中位线或把中线延长一倍来解决相关问题。
②在比例线段证明中,常作平行线。
作平行线时往往是保留结论中的一个比,然后通过一个中间比与结论中的另一个比联系起来。
③对于梯形问题,常用的添加辅助线的方法有
1、过上底的两端点向下底作垂线
2、过上底的一个端点作一腰的平行线
3、过上底的一个端点作一对角线的平行线
4、过一腰的中点作另一腰的平行线
5、过上底一端点和一腰中点的直线与下底的延长线相交
6、作梯形的中位线
7、延长两腰使之相交
四边形
平行四边形出现,对称中心等分点。
梯形里面作高线,平移一腰试试看。
平行移动对角线,补成三角形常见。
证相似,比线段,添线平行成习惯。
等积式子比例换,寻找线段很关键。
直接证明有困难,等量代换少麻烦。
斜边上面作高线,比例中项一大片。
关注收藏哦!
,