负数的定义
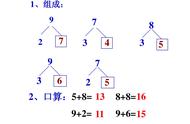
认识负数是很重要的一部分,我们先来看看小学教材中普遍是怎样引入负数的(看下图)。


可以看到主要是通过以下几个角度帮学生理解负数
- 通过零下温度呈现负数(如-20℃)。
- 通过海拔高度呈现负数(如-200米)。
- 通过相反方向呈现负数(如西-10米)。
- 通过收入支出呈现负数(如-100元)。
- 通过数线标出负数(如下图)。
总的来说,课本是通过“相反意义的量”帮助学生理解负数。其中利用温度计引入负数是教材中主要的例子,但是依靠温度计引入负数会出现新的问题。有了负数之后,自然我们需要比较负数的大小,理解负数的运算。
1. 比较大小中的问题
-20<-5
利用温度来理解就会出现矛盾,零下20度明明更冷,怎么会比零下5度小?
2. 负数运算中的问题
-(-1)=1
-1 (-1)=-2
我们知道两杯100度的沸水倒在一起并不是200度。所以温度计引入负数不能很好的解决这两个问题。
利用海拔高度可以观察到-5米比-20米要高,以此理解比较大小的问题,要比温度计好一些;利用数线上负数的位置比较大小更为直观,孩子们从一年级就知道数线上位置越往右的数越大。
但是 -(-1)=1还是不能严格证明。
最后教材中告诉我们10、2等这样的数都是正数,在这些数前面加上负号“-”的数,如-3、-500等就是负数。
所以教材中并没有严格地给出负数的定义,只是介绍了它的符号写法(看下图)。让学生知道了正数、负数表示具有相反意义的量。

我们发现小学教材是通过“相反意义的量”引入负数,初中教材普遍是怎么样引入的负数我们来看看(看下图)。