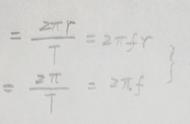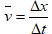F=ma=mv2/r=mω2r=mvω=m(2π/T)2r=m(2πn)2r
3.对公式的理解
(1)向心力公式既适用于匀速圆周运动,也适用于非匀速圆周运动。
(2)向心力公式具有瞬时性,即式中各量对应同一时刻。
(3)当m、ω一定时,由F知F∝r;
当m、v一定时,由F=mv2/r 知 F∝1/r。
特别提醒:
(1)在匀速圆周运动中,物体所受的合外力一定指向圆心,充当向心力。非匀速圆周运动的合外力不指向圆心,合外力的法向分力为向心力。
(2)任何情况的圆周运动,向心力的方向一定指向圆心,向心力是做圆周运动的物体需要的一个指向圆心的力,而不是物体又受到一个新的力。
【知识点4】 向心加速度
1、向心加速度
(1)定义:任何做匀速圆周运动的物体的加速度都指向圆心。这个加速度叫做向心加速度。
(2)公式:①an=v2/r;②an=ω2r。
(3)方向:沿半径方向指向圆心,时刻与线速度方向垂直。
2、向心加速度的方向及意义
(1)物理意义:
描述线速度改变的快慢,只表示线速度的方向变化的快慢,不表示其大小变化的快慢。
(2)方向:
总是沿着圆周运动的半径指向圆心,即方向始终与运动方向垂直,方向时刻改变。
(3)圆周运动的性质:
不论加速度an的大小是否变化,an的方向是时刻改变的,所以圆周运动一定是变加速曲线运动。
3、向心加速度的公式和应用
(1)公式
an=v2/r=ω2r=4π2r/T2=4π2n2r=4π2f 2r=ωv.
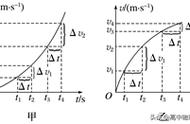
(2)an与r 的关系
图象如图所示:

(3)理解
①当匀速圆周运动的半径一定时,向心加速度的大小与角速度的平方成正比,也与线速度的平方成正比,随频率的增加或周期的减小而增大。
②当角速度一定时,向心加速度与运动半径成正比。
③当线速度一定时,向心加速度与运动半径成反比。
【知识点5】 生活中的圆周运动
一、车辆转弯
1.自行车(或摩托车)转弯
我们在骑自行车转弯时,有向外滑出的趋势,地面对自行车有指向内侧的静摩擦力F1,这个静摩擦力提供自行车转弯时所需的向心力。
根据向心力公式有F=F1=mv2/r,从公式中可以看出,转弯时所需的向心力与转弯时的速率及半径有关,如果转弯时的速率过大,静摩擦力不能满足转弯需要。
2.汽车转弯
汽车在水平路面上转弯时的向心力也来源于地面的静摩擦力,根据向心力公式有F=F1=mv2/r,转弯时所需的向心力与转弯时的速率及半径有关,如果转弯时的速率过大,静摩擦力不能满足转弯需要。
3.汽车在倾斜路面上转弯
车受重力mg及路面的弹力FN作用,这两个力的合力F水平并指向圆周弯道的圆心,充当向心力,
由图可知:F=mgtanθ,依据牛顿第二定律有 mgtanθ=mv2/r。

总结:(1)路面水平时转弯所需的向心力由静摩擦力力提供,若转弯半径为r,路面与车轮之间的最大静摩擦力为车重的k倍,汽车转弯的最大速度为

(2)高速公路的转弯处,公路的外沿设计得比内沿略高,若汽车以设计速度转弯时,汽车转弯的向心力由重力和弹力的合力提供.
4.火车转弯
(1)火车转弯时的特点:火车转弯时实际是在做圆周运动,因而具有向心加速度,需要向心力。
(2)向心力的来源
①如果转弯处内外轨一样高,则由外轨道对轮缘的弹力提供向心力,这样,铁轨和车轮极易受损。
②如果转弯处外轨略高于内轨,此时铁轨对火车的支持力不再是竖直的,而是斜向弯道内侧,它与重力的合力指向圆心,为火车转弯提供了一部分向心力,减轻了轮缘与外轨的挤压。适当设计内外轨的高度差,火车以规定的速度行驶时,转弯时所需的向心力几乎完全由重力与支持力的合力来提供。
二、航天器中的失重现象
航天员在航天器中绕地球做匀速圆周运动时,航天员只受地球引力,引力为他提供了绕地球做匀速圆周运动所需的向心力F=mv2/R,所以处于失重状态。
航天器绕地球做匀速圆周运动,假设它的线速度的大小为v,轨道半径近似等于地球半径R,航天员受到的地球引力近似等于他在地面测得的体重mg。
求:座舱对航天员的支持力为多少?
mg-FN=mv2/r,得FN=mg-mv2/r
当时V=