著名科学家牛顿说过:“在学习科学的时候,题目比规则还有用些”因此在他的著作中,每当阐述理论时,总是把许多实例放在一起。在牛顿的《普遍的算术》一书中,有一个关于求牛和头数的题目,人们称之为牛顿的牛吃草问题。
牛吃草问题主要类型: 1、求时间 2、求头数 除了总结这两种类型问题相应的解法,在实践中还要有培养运用“牛吃草问题”的解题思想解决实际问题的能力。
基本思路: ①在求出“每天新生长的草量”和“原有草量”后,已知头数求时间时,我们用“原有草量÷每天实际减少的草量(即头数与每日生长量的差)”求出天数。 ②已知天数求只数时,同样需要先求出“每天新生长的草量”和“原有草量”。 ③根据(“原有草量” 若干天里新生草量)÷天数”,求出只数。
解决牛吃草问题常用到四个基本公式,分别是∶
(1)草的生长速度=对应的牛头数×吃的较多天数-相应的牛头数×吃的较少天数÷(吃的较多天数-吃的较少天数); (2)原有草量=牛头数×吃的天数-草的生长速度×吃的天数; (3)吃的天数=原有草量÷(牛头数-草的生长速度); (4)牛头数=原有草量÷吃的天数+草的生长速度
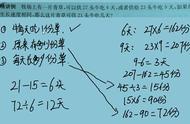
第一种:一般解法。问☞有一牧场,已知养牛27头,6天把草吃尽;养牛23头,9天把草吃尽。如果养牛21头,那么几天能把牧场上的草吃尽呢?并且牧场上的草是不断生长的。”解答:把一头牛一天所吃的牧草看作1,那么就有: (1)27头牛6天所吃的牧草为:27×6=162 (这162包括牧场原有的草和6天新长的草。) (2)23头牛9天所吃的牧草为:23×9=207 (这207包括牧场原有的草和9天新长的草。) (3)1天新长的草为:(207-162)÷(9-6)=15 (4)牧场上原有的草为:27×6-15×6=72 (5)每天新长的草足够15头牛吃,21头牛减去15头,剩下6头吃原牧场的草:72÷(21-15)=72÷6=12(天) 所以养21头牛,12天才能把牧场上的草吃
第二种:公式解法,问☞有一片牧场,草每天都匀速生长(草每天增长量相等),如果放牧24头牛,则6天吃完牧草,如果放牧21头牛,则8天吃完牧草,假设每头牛吃草的量是相等的。(1)如果放牧16头牛,几天可以吃完牧草?(2)要使牧草永远吃不完,最多可放多少头牛?解答: 1) 草的生长速度:(21×8-24×6)÷(8-6)=12(份) 原有草量:21×8-12×8=72(份) 16头牛可吃:72÷(16-12)=18(天) 2) 要使牧草永远吃不完,则每天吃的份数不能多于草每天的生长份数 所以最多只能放12头牛。
下面我给大家找了3道奥赛题中的牛吃草问题,大家可以对照着理解理解。
,