我们为什么要研究牛吃草问题?
通过这边文章,你希望能获得什么?能获得什么?
你有期望吗,有目标吗?
读完你的目的实现了吗?欢迎留言分享您的看法和宝贵意见!
本文将主要从以下个方面讲述牛吃草问题:
1,牛吃草及其相关问题
2,牛吃草问题的3种解法
3,牛吃草问题的3种变形
1.牛吃草问题的描述
牛吃草问题也称消长问题或牛顿问题,是伟大的科学家牛顿提出来的,在其著作《算数》中,有这么一道题目:
有一片牧场,已知牛27头,6天把草吃光;牛23头,9天吃光。如果有牛21头,几天能把草吃光?
牛吃草问题是小学数学应用题中难度较高的题目,如果没有了解过,学生们往往束手无策。当然从环保及可持续发展的角度来说,把草吃光可不是个好主意。
2.牛吃草问题的隐藏条件
牛吃草问题中,有隐藏条件,即牛在吃草,草在生长,牛吃草的速度大于草生长的速度,那么草终究会被吃光。吃草的牛越多,草被吃光花的时间越短。牛吃草问题中的不变量:草地原有草量、牛吃草速度、草生长速度不变。
当然题目中并没有给出这些信息,这些是我们为了解决问题而做出的合理化假设,把实际问题变成数学问题的时候,我们需要做一些合理化的假设,这也叫建模(建立数学模型)。
3.与牛吃草问题相似的问题
牛吃草问题也称消长问题,顾名思义,此消彼长。
如果我们把牛吃草看成是牛需要做的工作,牛吃草问题就变成了工程问题。
如果我们把草铺成一条道路,牛在道路的这头,道路的那头的草不停的生长,牛吃草问题就变成追及问题。
同样类似的,船漏水舀水,闸口放行都可以看出牛吃草问题处理。
了解了什么是牛吃草问题,我们看如何解决牛吃草问题,本文提供三种解法。
二,牛吃草问题的几种解法1,常规算数解法(1个假设,1个核心关系式,需掌握)
假设:一头牛一天吃掉的草量为1。
核心关系式:牛共吃掉的草量=原有草量 新生长草量
分析:把题目中的已知条件代入关系式,研究各个量之间的关系。
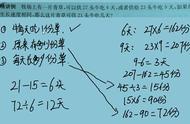
牛27头,6天吃光,即,27头牛6天吃掉的草量=原有草量 6天生长草量,代入数据有:
27×6=原有草量 6×每天生长草量..............................①
牛23头,9天吃光,即,23头牛9天吃掉的草量=原有草量 9天生长草量,代入数据有:
23×9=原有草量 9×每天生长草量..............................②
比较①②式可知,两次吃草的时间差为9-6=3(天),总草量的差为23×9-27×6=45,也就是3天生长的草量为45,那么一天生长的草量为45÷3=15。
根据①式可知:
原有草量=27×6-6×每天生长草量
=27×6-6×15
=72
回归到问题:如果有牛21头,几天能把草吃光?
核心关系式依然成立,直接代入数据有:
21×?=原有草量 ?×每天生长草量
21×?=72 ?×15
这里,我们如果学过一元一次方程,我们直接用方程解即可。
如果没有学过方程,或者掌握不好,可以这么理解:21头牛一天吃21份草,而草地每天长15份草,两者抵消,相当于每天能吃净草21-15=6(份),草地共有净草72份,共需吃72÷6=12(天)。
(这里有没有熟悉的感觉,72就是追及问题中的追及路程,而21-15就是速度差,牛吃完草的时候就是追上的时候。)
总结:①②式我们称之为关系式,在工程问题中也可以用类似的方法帮助我们整理思路,而且可以更好的想方程思维过度,帮助学生从整体上把握题目的走向。
牛吃草问题我们这里不提供任何公式,关键需要理清其将实际问题转化为数学问题过程中做的一些假设,以及基本关系式,这些关系式既有生活常识,也有理性思维,需要保持对生活的观察和思考的热情。
方法1的拓展(以下分割线内有能力的学生可以参考了解)
- 利用二元一次方程,部分有能力的学生或许已经接触过或者有能力接受,当我们把2.1中①②两式中的“原有草量”用x代替,“每天生长草量”用y代替,则可得二元一次方程:
23×9=x 6y..............................①'
23×9=x 9y............................②'
②'-①'有:
23×9-23×9=9y-6y
y=15,
代入式①'有:
x=72
后面的计算同方法1。
(当然,我们也可以设21头牛吃完草的天数设为z,在利用一次核心关系式,就变成了三元一次方程,有兴趣和能力的同学可以尝试。)
- 看成追及问题解答

如图:在前面的描述中,我们已经知道,原有草量可以类比为追及问题中的追及路程,牛在追,草在长。
我们重新设定这道题目:
牛从A地出发,草从B地出发,牛的速度是27,6天追上草;牛的速度是23,9天追上草。当牛的速度是21,几天追上草?
分析:本题中,牛的速度在变,而草的速度不变,追及路程不变。
追及路程=速度差×追及时间
由3次追及中追及路程相等作为等量关系,有:
(27-V草)×6=(23-V草)×9
(也可理解为速度差和追及时间成反比例)
解方程可得V草,代入追及路程公式可得原有草量,再用公式可得V牛=21时的追及时间。
2,分数解法(基础较好的同学掌握)
鉴于分数在小学中的重要性,此方法是对分数应用基本功的一种检验。小学五六年级,分数计算及应用是核心,单位1的量的又是其中的重难点。所以,牛吃草问题的第二种解法我们从分数的角度来分析求解。
思路1(跟方法1的思路类似):
设27头牛6天吃草总量为单位1,则一头牛一天吃草的量为:

23头牛9天吃草: