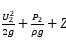2、同一流管的任意截面伯努利方程


含义:对于理想流体作稳定流动,在同一流管中任一处,每单位体积流体的动能、势能和该处压强之和是一个衡量。
- 伯努利方程是理想流体作稳定流动时的基本方程;
- 对于实际流体,如果粘滞性很小,如:水、空气、酒精等,可应用伯努利方程解决实际问题;
- 对于确定流体内部各处的压力和流速有很大的实际意义,在水利、造船、航空等部门有着广泛的应用。
需要注意的是,由于伯努利方程是由机械能守恒推导出的,所以它仅适用于黏性可以忽略、不可被压缩的理想流体。在粘性流体流动中,粘性摩擦力因消耗机械能而产生热,机械能不守恒,在推广使用伯努利方程时,应加进机械能损失项。
二、应用篇——伯努利方程的广泛使用
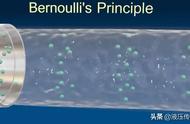
丹尼尔·伯努利在1726年提出了“伯努利原理”,是流体动力学基本方程之一。伯努利方程是理想流体定常流动的动力学方程,解释为不可被压缩的流体在忽略粘性损失的流动中,流线上任意两点的压力势能、动能与位势能之和保持不变。其实质是流体的机械能守恒,即:动能 重力势能 压力势能=常数。对于水泵来说就是:速度头 静压头 位置头=常数。
其最为著名的推论为:等高度流动时,流速大,压力就小。
1、翼型升力