因此结果是:

这表明对于一个多项式f(x),当被另一个非零得多项式d(x)相除时,其商为q(x), 余项为r(x), 那么:

上面的d(x)的阶数要比f(x)小,r(x)的阶数不会高于d(x)的阶数 (所谓阶数就是多项式的最高幂次)。如果d(x)=x-k, 那么就有 f(x)=(x-k)q(x) r

至此我们可以给出余数定理:
若多项式f(x)被x-k相除,那么余数是f(k)。
这个定理很容易证明, 将x=k带入f(x)=(x-k)q(x) r 有:

因此结果是:

这表明对于一个多项式f(x),当被另一个非零得多项式d(x)相除时,其商为q(x), 余项为r(x), 那么:

上面的d(x)的阶数要比f(x)小,r(x)的阶数不会高于d(x)的阶数 (所谓阶数就是多项式的最高幂次)。如果d(x)=x-k, 那么就有 f(x)=(x-k)q(x) r

至此我们可以给出余数定理:
若多项式f(x)被x-k相除,那么余数是f(k)。
这个定理很容易证明, 将x=k带入f(x)=(x-k)q(x) r 有:







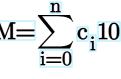

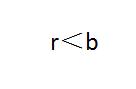





Copyright © 2018 - 2021 www.yd166.com., All Rights Reserved.